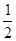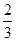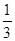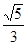题目内容
若焦点在 轴上的椭圆
轴上的椭圆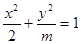 的离心率为
的离心率为 ,则
,则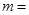 ( )
( )
A.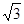 | B.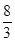 | C.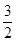 | D.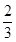 |
C
解析试题分析:由于焦点在 轴上的椭圆,则可知
轴上的椭圆,则可知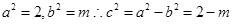 ,由于离心率为
,由于离心率为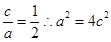 ,故得到2=4(2-m),解得m=
,故得到2=4(2-m),解得m=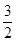 ,故选C.
,故选C.
考点:本题主要考查了椭圆的性质的运用。
点评:解决该试题的关键是理解方程中的,a,b的值,结合离心率的性质得到a,c的比值关系式,进而得到参数m的值。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
设P是双曲线 与圆
与圆 在第一象限的交点,
在第一象限的交点, 分别是双曲线的左右焦点,且
分别是双曲线的左右焦点,且 则双曲线的离心率为( )
则双曲线的离心率为( )
A. | B. | C.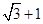 | D.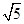 |
已知抛物线 ,点P在此抛物线上,则P到直线
,点P在此抛物线上,则P到直线 和
和 轴的距离之和的最小值
轴的距离之和的最小值
是( )
A. | B. | C.2 | D. |
已知AB是过椭圆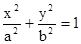 (a>b>0)的左焦点F1的弦,则⊿ABF2的周长是( )
(a>b>0)的左焦点F1的弦,则⊿ABF2的周长是( )
| A.a | B.2a | C.3ª | D.4a |
双曲线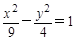 与直线
与直线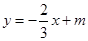 (
(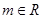 )的公共点的个数为( ).
)的公共点的个数为( ).
| A.0 | B.1 | C.0或1 | D.0或1或2 |
已知方程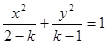 的图象是双曲线,那么k的取值范围是( )
的图象是双曲线,那么k的取值范围是( )
A.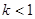 | B.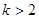 | C.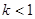 或 或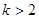 | D. |
抛物线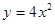 上一点到直线
上一点到直线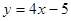 的距离最短,则该点的坐标是( )
的距离最短,则该点的坐标是( )
| A.(1, 2) | B.(0, 0) | C.(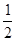 , 1) , 1) | D.(1, 4) |
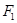 和
和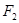 为双曲线
为双曲线
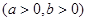 的两个焦点, 若
的两个焦点, 若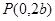 是正三角形的三个顶点,则双曲线的离心率为 ( )
是正三角形的三个顶点,则双曲线的离心率为 ( ) 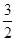


 上一点,若
上一点,若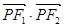 =0,
=0, 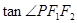 =2,则椭圆的离心率为( )
=2,则椭圆的离心率为( )