题目内容
12.C是曲线y=$\sqrt{1-{x^2}}$(x≤0)上点,CD⊥y轴,D是垂足,A点坐标是(-1,0),设∠CAO=θ(其中O为原点),将AC+CD表示成关于θ的函数f(θ),则f(θ)=( )| A. | 2cosθ-cos2θ | B. | cosθ+sinθ | C. | 2cosθ(1+cosθ) | D. | 2sinθ+cosθ-$\sqrt{2}$ |
分析 由题意作出图形,再连结CO,从而可得点C的坐标为(-cos(180°-2θ),sin(180°-2θ));从而化简可得f(θ)=2cosθ-cos2θ.
解答 解:如图,连结CO,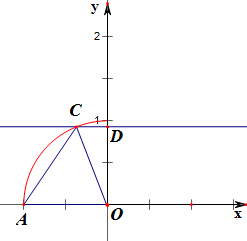
∵∠CAO=θ,
∴∠COA=180°-2θ,
∴点C的坐标为(-cos(180°-2θ),sin(180°-2θ));
即点C的坐标为(cos2θ,sin2θ);
∴AC=$\sqrt{(cos2θ+1)^{2}+{sin}^{2}2θ}$=$\sqrt{2(1+cos2θ)}$=2|cosθ|
=2cosθ,
CD=|cos2θ|=-cos2θ,
f(θ)=2cosθ-cos2θ,
故选:A.
点评 本题考查了三角函数的性质与应用及三角恒等变换的应用,同时考查了函数的最值的求法,属于中档题

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
2.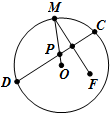 如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )
如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )
 如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )
如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
2.已知命题p:“?x>0,ex≥1”,则¬p为( )
| A. | ?x≤0,使得ex≤1 | B. | ?x≤0,使得ex<1 | C. | ?x>0,使得ex<1 | D. | ?x>0,使得ex≤1 |