题目内容
2．已知命题p：“?x＞0，ex≥1”，则￢p为（ ）| A． | ?x≤0，使得ex≤1 | B． | ?x≤0，使得ex＜1 | C． | ?x＞0，使得ex＜1 | D． | ?x＞0，使得ex≤1 |
分析 根据全称命题 的否定为特称命题可写出命题p的否定．
解答 解：根据全称命题P：?x＞0，ex≥1的否定为特称命题，
即：￢p为?x＞0，ex＜1．
故选：C．
点评 本题主要考查了全称命题的否定的写法，对量词及结论都要进行否定．
练习册系列答案
相关题目
12．C是曲线y=$\sqrt{1-{x^2}}$（x≤0）上点，CD⊥y轴，D是垂足，A点坐标是（-1，0），设∠CAO=θ（其中O为原点），将AC+CD表示成关于θ的函数f（θ），则f（θ）=（ ）
| A． | 2cosθ-cos2θ | B． | cosθ+sinθ | C． | 2cosθ（1+cosθ） | D． | 2sinθ+cosθ-$\sqrt{2}$ |
13．计算$\frac{tan\frac{π}{8}}{{1-tan}^{2}\frac{π}{8}}$的结果是（ ）
| A． | 1 | B． | 2 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
10．
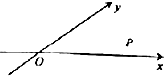如图，a∈（0，π），且a≠$\frac{π}{2}$，当∠xOy=e时，定义平面坐标系xOy为a仿射坐标系，在α-仿射坐标系中，任意一点P的斜坐标这样定义：$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量，若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，则记为$\overrightarrow{OP}$=（x，y），若在仿射坐标系中，已知$\overrightarrow{a}$=（m，n），$\overrightarrow{b}$=（s，t），下列结论中不正确的是（ ）
如图，a∈（0，π），且a≠$\frac{π}{2}$，当∠xOy=e时，定义平面坐标系xOy为a仿射坐标系，在α-仿射坐标系中，任意一点P的斜坐标这样定义：$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别为与x轴、y轴正向相同的单位向量，若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，则记为$\overrightarrow{OP}$=（x，y），若在仿射坐标系中，已知$\overrightarrow{a}$=（m，n），$\overrightarrow{b}$=（s，t），下列结论中不正确的是（ ）| A． | 若$\overrightarrow{a}$=$\overrightarrow{b}$，则m=s，n=t | |
| B． | 若$\overrightarrow{a}$$∥\overrightarrow{b}$，则mt-ns=0 | |
| C． | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则ms+nt=0 | |
| D． | 若m=t=1，n=s=2，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角$\frac{π}{3}$，则a=$\frac{2π}{3}$ |
17．已知ξ～N（3，σ2），若P（ξ≤2）=0.2，则P（ξ≤4）等于（ ）
| A． | 0.2 | B． | P（-2≤ξ≤2）=0.4 | C． | P（ξ＞2）=0.2 | D． | P（ξ≤4）=0.8 |
14．设函数g（x）=x2（x∈R），f（x）=$\left\{\begin{array}{l}{g（x）+1，x＜g（x）}\\{g（x）-x，x≥g（x）}\end{array}\right.$，则函数f（x）的值域是（ ）
| A． | [-$\frac{1}{4}$，+∞） | B． | [0，+∞） | C． | [$-\frac{1}{4}$，0]∪（2，+∞） | D． | [-$\frac{1}{4}$，0]∪（1，+∞） |