题目内容
设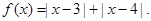
(1)解不等式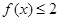 ;
;
(2)若存在实数x满足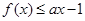 ,试求实数a的取值范围。
,试求实数a的取值范围。
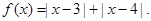
(1)解不等式
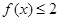 ;
;(2)若存在实数x满足
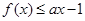 ,试求实数a的取值范围。
,试求实数a的取值范围。(Ⅰ){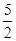 ,
,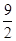 ]. (Ⅱ) (-∞,-2)∪[
]. (Ⅱ) (-∞,-2)∪[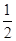 ,+∞)
,+∞)
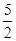 ,
,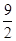 ]. (Ⅱ) (-∞,-2)∪[
]. (Ⅱ) (-∞,-2)∪[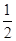 ,+∞)
,+∞)本试题主要是考查了绝对值不等式的运用和求解的综合运用。结合了分段函数的图像与图像的交点的综合运用。
(1)对于f(x)=|x-3|+|x-4|,利用三段论,作函数y=f(x)的图象,它与直线y=2交点的横坐标为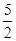 和
和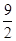 ,由图象知不等式f(x)≤2的解集为[
,由图象知不等式f(x)≤2的解集为[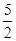 ,
,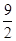 ].
].
(2)函数y=ax-1的图象是过点(0,-1)的直线.
当且仅当函数y=f(x)与直线y=ax-1有公共点时,结合图像得到结论
解:(Ⅰ)f(x)=|x-3|+|x-4|=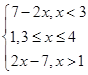 …2分
…2分
作函数y=f(x)的图象,它与直线y=2交点的横坐标为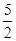 和
和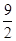 ,由图象知
,由图象知
不等式f(x)≤2的解集为[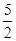 ,
,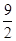 ]. …5分
]. …5分
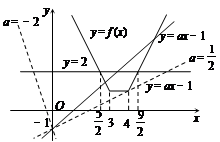
(Ⅱ)函数y=ax-1的图象是过点(0,-1)的直线.
当且仅当函数y=f(x)与直线y=ax-1有公共点时,存在题设的x.
由图象知,a取值范围为(-∞,-2)∪[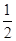 ,+∞)
,+∞)
(1)对于f(x)=|x-3|+|x-4|,利用三段论,作函数y=f(x)的图象,它与直线y=2交点的横坐标为
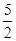 和
和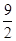 ,由图象知不等式f(x)≤2的解集为[
,由图象知不等式f(x)≤2的解集为[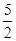 ,
,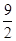 ].
]. (2)函数y=ax-1的图象是过点(0,-1)的直线.
当且仅当函数y=f(x)与直线y=ax-1有公共点时,结合图像得到结论
解:(Ⅰ)f(x)=|x-3|+|x-4|=
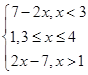 …2分
…2分作函数y=f(x)的图象,它与直线y=2交点的横坐标为
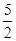 和
和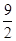 ,由图象知
,由图象知不等式f(x)≤2的解集为[
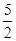 ,
,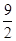 ]. …5分
]. …5分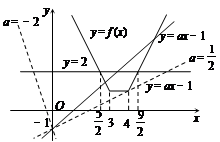
(Ⅱ)函数y=ax-1的图象是过点(0,-1)的直线.
当且仅当函数y=f(x)与直线y=ax-1有公共点时,存在题设的x.
由图象知,a取值范围为(-∞,-2)∪[
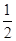 ,+∞)
,+∞)
练习册系列答案
相关题目
 使不等式
使不等式 成立,则实数
成立,则实数 的取值范围是_____________.
的取值范围是_____________.
 中,曲线
中,曲线 与
与 的交点的极坐标为_.
的交点的极坐标为_.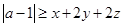 ,对满足
,对满足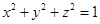 的一切实数
的一切实数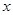 、
、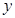 、
、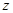 恒成立,则实数a的取值范围 .
恒成立,则实数a的取值范围 . 的最小值.
的最小值. 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围. 恒成立.则a与b满足的关系是____.
恒成立.则a与b满足的关系是____.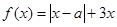 ,其中
,其中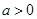 。
。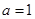 时,求不等式
时,求不等式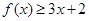 的解集
的解集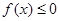 的解集为
的解集为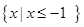 ,求a的值。
,求a的值。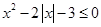 的解集为
的解集为 
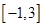
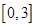
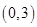
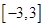
 的最小值为( )
的最小值为( )