题目内容
不等式|x-5|+|x+3|≥10的解集是( )
| A.[-5,7] | B.[-4,6] |
| C.(-∞,-5]∪[7,+∞) | D.(-∞,-4]∪[6,+∞) |
D
解:法一:当x=0时,|x-5|+|x+3|=8≥10不成立
可排除A,B
当x=-4时,|x-5|+|x+3|=12≥12成立
可排除C
故选D
法二:当x<-3时
不等式|x-5|+|x+3|≥10可化为:-(x-5)-(x+3)≥10
解得:x≤-4
当-3≤x≤5时
不等式|x-5|+|x+3|≥10可化为:-(x-5)+(x+3)=8≥10恒不成立
当x>5时
不等式|x-5|+|x+3|≥10可化为:(x-5)+(x+3)≥10
解得:x≥6
故不等式|x-5|+|x+3|≥10解集为:(-∞,-4]∪[6,+∞)
故选D
可排除A,B
当x=-4时,|x-5|+|x+3|=12≥12成立
可排除C
故选D
法二:当x<-3时
不等式|x-5|+|x+3|≥10可化为:-(x-5)-(x+3)≥10
解得:x≤-4
当-3≤x≤5时
不等式|x-5|+|x+3|≥10可化为:-(x-5)+(x+3)=8≥10恒不成立
当x>5时
不等式|x-5|+|x+3|≥10可化为:(x-5)+(x+3)≥10
解得:x≥6
故不等式|x-5|+|x+3|≥10解集为:(-∞,-4]∪[6,+∞)
故选D

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
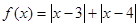 .
.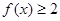 的解集;
的解集;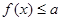 的解集不是空集,求实数
的解集不是空集,求实数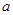 的取值范围.
的取值范围.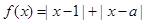 ,
,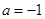 ,解不等式
,解不等式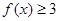 ;(2)如果
;(2)如果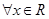 ,
,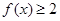 ,求a的取值范围。
,求a的取值范围。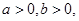 且
且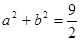 ,若
,若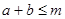 恒成立,
恒成立,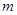 的最小值;
的最小值;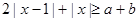 对任意的
对任意的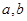 恒成立,求实数
恒成立,求实数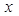 的取值范围.
的取值范围.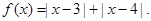
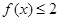 ;
;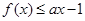 ,试求实数a的取值范围。
,试求实数a的取值范围。 的解集为M,且2
的解集为M,且2 M,则
M,则 的取值范围是( )
的取值范围是( ) ]
]

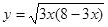 (
(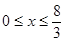 )的最大值是
)的最大值是 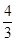
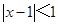 的解集是____________.
的解集是____________.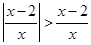 解集是 ( )
解集是 ( )