题目内容
设函数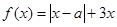 ,其中
,其中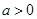 。
。
(Ⅰ)当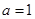 时,求不等式
时,求不等式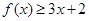 的解集
的解集
(Ⅱ)若不等式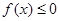 的解集为
的解集为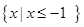 ,求a的值。
,求a的值。
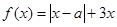 ,其中
,其中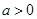 。
。(Ⅰ)当
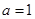 时,求不等式
时,求不等式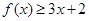 的解集
的解集(Ⅱ)若不等式
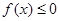 的解集为
的解集为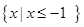 ,求a的值。
,求a的值。 (1)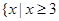 或
或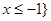 (2)
(2)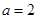
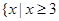 或
或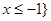 (2)
(2)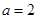
解含绝对值的不等式的基本思想是等价转化,即采用正确的方法去掉绝对值符号转化为不含绝对值的不等式来解,常用的方法有公式法、定义法、平方法、零点分段讨论法、几何意义等
(Ⅰ)当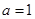 时,
时,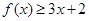 可化为
可化为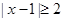 。由此可得
。由此可得 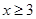 或
或 。
。
故不等式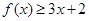 的解集为
的解集为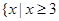 或
或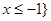 。
。
( Ⅱ) 由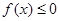 得
得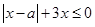
此不等式化为不等式组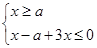 或
或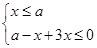 即
即 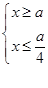 或
或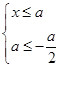
因为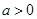 ,所以不等式组的解集为
,所以不等式组的解集为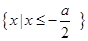 由题设可得
由题设可得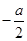 =
= 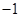 ,故
,故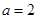
(Ⅰ)当
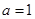 时,
时,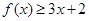 可化为
可化为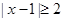 。由此可得
。由此可得 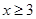 或
或 。
。故不等式
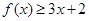 的解集为
的解集为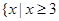 或
或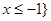 。
。( Ⅱ) 由
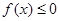 得
得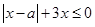
此不等式化为不等式组
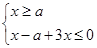 或
或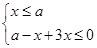 即
即 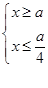 或
或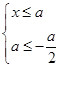
因为
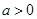 ,所以不等式组的解集为
,所以不等式组的解集为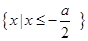 由题设可得
由题设可得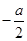 =
= 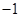 ,故
,故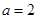

练习册系列答案
相关题目
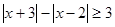 的解集为____________
的解集为____________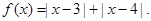
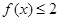 ;
;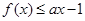 ,试求实数a的取值范围。
,试求实数a的取值范围。 的解集为M,且2
的解集为M,且2 M,则
M,则 的取值范围是( )
的取值范围是( ) ]
]

 的方程分别为:
的方程分别为: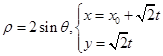 (t为参数)。若圆C被直线
(t为参数)。若圆C被直线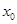 的值为 。
的值为 。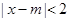 成立的充分不必要条件是
成立的充分不必要条件是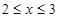 ,则实数m的取值范围是______________。
,则实数m的取值范围是______________。 .
.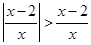 解集是 ( )
解集是 ( )