题目内容
(本小题满分12分)如图,在三棱锥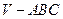 中,
中,
 底面
底面 ,
, ,
,
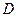 是
是 的中点,且
的中点,且 ,
,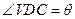
 .
.
(1)求证:平面 平面
平面 ;(2)当角
;(2)当角 变化时,求直线
变化时,求直线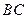 与平面
与平面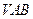 所成的角
所成的角
的取值范围。
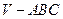 中,
中, 底面
底面 ,
, ,
,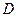 是
是 的中点,且
的中点,且 ,
,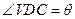
 .
.(1)求证:平面
 平面
平面 ;(2)当角
;(2)当角 变化时,求直线
变化时,求直线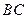 与平面
与平面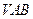 所成的角
所成的角的取值范围。
(Ⅰ)略 (Ⅱ)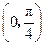
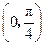
(1)
 是等腰三角形,
是等腰三角形,
又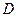 是
是 的中点
的中点  ,又
,又 底面
底面
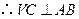
于是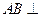 平面
平面 .又
.又 平面
平面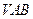
 平面
平面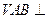 平面
平面 ┈5分
┈5分
 2)过点
2)过点 在平面
在平面 内作
内作 于
于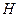 ,连接
,连接 ,则由1)知AB⊥CH, ∴CH⊥平面
,则由1)知AB⊥CH, ∴CH⊥平面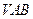 ,于是
,于是 就是直线
就是直线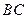 与平面
与平面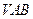 所成的角,在
所成的角,在 中,CD=
中,CD=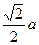 ,
,  ;设
;设 ,在
,在 中,
中, ,
,
 ,
,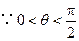 ,
, ,
,
 ,又
,又 ,
,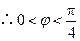
即直线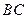 与平面
与平面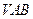 所成角的取值范围为
所成角的取值范围为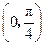 .
.
解法2:1)以 所在的直线分别为
所在的直线分别为 轴、
轴、 轴、
轴、 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则 ,
,
于是, ,
, ,
, .
.
从而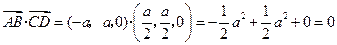 ,即
,即 .
.
 同理
同理 ,
,
即 .又
.又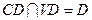 ,
, 平面
平面 .又
.又 平面
平面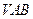 .
.
 平面
平面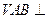 平面
平面 .
.
2)设直线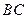 与平面
与平面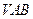 所成的角为
所成的角为 ,平面
,平面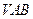 的一个法向
的一个法向
量为 ,则由
,则由 .
.
得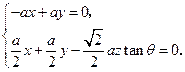 可取
可取 ,又
,又 ,
,
于是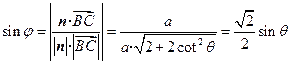 ,
,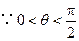 ,
, ,
, .又
.又 ,
,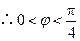 .
.
即直线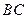 与平面
与平面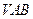 所成角的取值范围为
所成角的取值范围为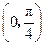 .
.

 是等腰三角形,
是等腰三角形,又
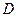 是
是 的中点
的中点  ,又
,又 底面
底面
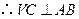
于是
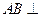 平面
平面 .又
.又 平面
平面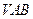
 平面
平面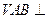 平面
平面 ┈5分
┈5分 2)过点
2)过点 在平面
在平面 内作
内作 于
于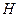 ,连接
,连接 ,则由1)知AB⊥CH, ∴CH⊥平面
,则由1)知AB⊥CH, ∴CH⊥平面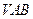 ,于是
,于是 就是直线
就是直线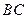 与平面
与平面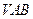 所成的角,在
所成的角,在 中,CD=
中,CD=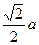 ,
,  ;设
;设 ,在
,在 中,
中, ,
, ,
,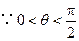 ,
, ,
, ,又
,又 ,
,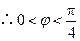
即直线
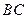 与平面
与平面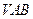 所成角的取值范围为
所成角的取值范围为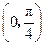 .
.解法2:1)以
 所在的直线分别为
所在的直线分别为 轴、
轴、 轴、
轴、 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则 ,
,于是,
 ,
, ,
, .
.从而
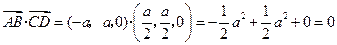 ,即
,即 .
. 同理
同理 ,
,即
 .又
.又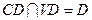 ,
, 平面
平面 .又
.又 平面
平面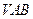 .
. 平面
平面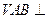 平面
平面 .
.2)设直线
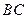 与平面
与平面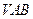 所成的角为
所成的角为 ,平面
,平面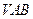 的一个法向
的一个法向量为
 ,则由
,则由 .
.得
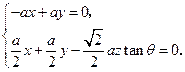 可取
可取 ,又
,又 ,
,于是
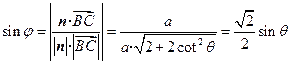 ,
,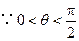 ,
, ,
, .又
.又 ,
,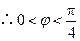 .
.即直线
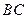 与平面
与平面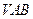 所成角的取值范围为
所成角的取值范围为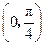 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 的长;
的长; >的值;
>的值; 的棱长为
的棱长为 ,过点
,过点 作平面
作平面 的垂线,垂足为点
的垂线,垂足为点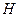 ,则以下命题中,错误的命题是( )
,则以下命题中,错误的命题是( )
 的垂心
的垂心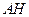 垂直平面
垂直平面

 所成角为
所成角为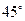
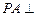 ⊙O所在的平面,
⊙O所在的平面, 是⊙O的直径,
是⊙O的直径,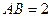 ,
, C是⊙O上一点,且
C是⊙O上一点,且 ,
, 与⊙O所在的平面成
与⊙O所在的平面成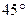 角,
角, 是
是 ;(Ⅱ) 求证:
;(Ⅱ) 求证: ;
;