题目内容
在四棱锥P—ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.
(1)使∠PED=90°;
(2)使∠PED为锐角. 证明你的结论.
(1)使∠PED=90°;
(2)使∠PED为锐角. 证明你的结论.
(1))当AB≤ AD时,边BC上存在点E,使∠PED=90°;当AB>
AD时,边BC上存在点E,使∠PED=90°;当AB> AD时,使∠PED=90°的点E不存在.(2)边BC上总存在一点,使∠PED为锐角,点B就是其中一点
AD时,使∠PED=90°的点E不存在.(2)边BC上总存在一点,使∠PED为锐角,点B就是其中一点
 AD时,边BC上存在点E,使∠PED=90°;当AB>
AD时,边BC上存在点E,使∠PED=90°;当AB> AD时,使∠PED=90°的点E不存在.(2)边BC上总存在一点,使∠PED为锐角,点B就是其中一点
AD时,使∠PED=90°的点E不存在.(2)边BC上总存在一点,使∠PED为锐角,点B就是其中一点 (1)当AB≤ AD时,边BC上存在点E,使∠PED=90°;当AB>
AD时,边BC上存在点E,使∠PED=90°;当AB> AD时,使∠PED=90°的点E不存在.(只须以AD为直径作圆看该圆是否与BC边有无交点)(证略)
AD时,使∠PED=90°的点E不存在.(只须以AD为直径作圆看该圆是否与BC边有无交点)(证略)
(2)边BC上总存在一点,使∠PED为锐角,点B就是其中一点.
连接BD,作AF⊥BD,垂足为F,连PF,∵PA⊥面ABCD,∴PF⊥BD,又△ABD为直角三角形,∴F点在BD上,∴∠PBF是锐角. 同理,点C也是其中一点.
 AD时,边BC上存在点E,使∠PED=90°;当AB>
AD时,边BC上存在点E,使∠PED=90°;当AB> AD时,使∠PED=90°的点E不存在.(只须以AD为直径作圆看该圆是否与BC边有无交点)(证略)
AD时,使∠PED=90°的点E不存在.(只须以AD为直径作圆看该圆是否与BC边有无交点)(证略)(2)边BC上总存在一点,使∠PED为锐角,点B就是其中一点.
连接BD,作AF⊥BD,垂足为F,连PF,∵PA⊥面ABCD,∴PF⊥BD,又△ABD为直角三角形,∴F点在BD上,∴∠PBF是锐角. 同理,点C也是其中一点.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 中,
中, ,
,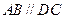 ,且满足
,且满足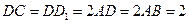

 平面
平面 ;
; 的余弦值。
的余弦值。
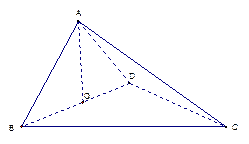
 .
.  平面BCD;
平面BCD; 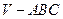 中,
中,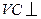 底面
底面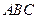 ,
,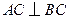 ,
,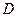 是
是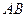 的中点,且
的中点,且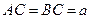 ,
,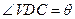
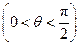 .
.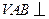 平面
平面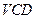 ;(2)当角
;(2)当角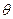 变化时,求直线
变化时,求直线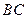 与平面
与平面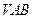 所成的角
所成的角

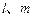 与平面
与平面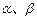 的命题中,真命题是( )
的命题中,真命题是( ) 且
且 ,则
,则
 且
且 ,则
,则
 且
且 ,则
,则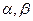 ,有以下四个命题:
,有以下四个命题: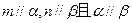 ,则
,则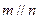
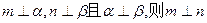 ;
;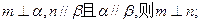
 ;
;