题目内容
在平面直角坐标系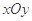 中,动点
中,动点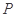 到两点
到两点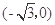 ,
,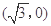 的距离之和等于
的距离之和等于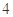 ,设点
,设点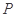 的轨迹为曲线
的轨迹为曲线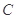 ,直线
,直线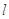 过点
过点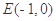 且与曲线
且与曲线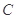 交于
交于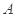 ,
,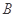 两点.
两点.
(1)求曲线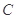 的轨迹方程;
的轨迹方程;
(2)是否存在△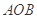 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△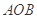 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
(1)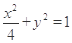 ;(2)存在
;(2)存在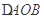 面积的最大值为
面积的最大值为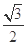 .
.
解析试题分析:(1)根据椭圆的性质易得椭圆方程;(2)先设过点E的直线方程,然后把直线方程和椭圆方程联立得关于y的一元二次方程,解出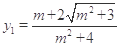 ,
,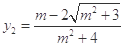 ,则
,则 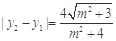 ,从而得△
,从而得△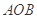 面积的表达式,再由不等式性质求得面积最大值.
面积的表达式,再由不等式性质求得面积最大值.
试题解析:(1)由椭圆定义可知,点P的轨迹C是以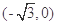 ,
,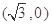 为焦点,
为焦点,
长半轴长为2的椭圆, 3分
故曲线C的方程为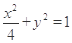 . 6分
. 6分
(2)存在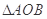 面积的最大值. 7分
面积的最大值. 7分
因为直线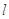 过点
过点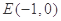 ,可设直线
,可设直线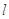 的方程为
的方程为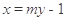 或
或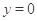 (舍),
(舍),
则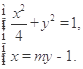 整理得
整理得 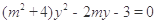 . 8分
. 8分
由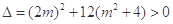 .设
.设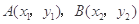 .
.
解得 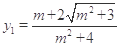 ,
, 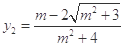 .则
.则 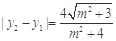 .
.
因为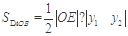
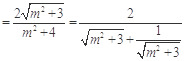 . 11分
. 11分
设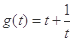 ,
,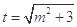 ,
,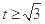 .
.
则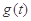 在区间
在区间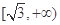 上为增函数.所以
上为增函数.所以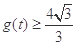 .
.
所以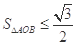 ,当且仅当
,当且仅当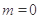 时取等号,即
时取等号,即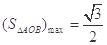 .
.
所以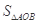 的最大值为
的最大值为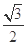 . 14分
. 14分
考点:1、椭圆的标准方程及性质;2、直线与椭圆相交问题;3、不等式的性质.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
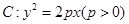 的焦点为
的焦点为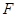 ,准线为
,准线为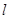 ,
,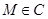 ,以
,以 为圆心的圆
为圆心的圆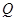 ,
,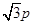 ,
, 是圆
是圆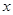 轴除
轴除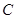 与圆
与圆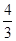 的直线
的直线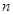 与
与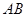 两点,求
两点,求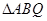 的面积.
的面积.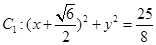 ,圆
,圆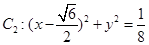 ,动圆
,动圆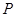 与已知两圆都外切.
与已知两圆都外切.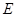 的方程;
的方程; 与点
与点 、
、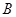 ,
,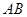 的中垂线与
的中垂线与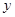 轴交于点
轴交于点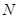 ,求点
,求点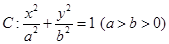 的右焦点为
的右焦点为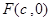 ,上顶点为B,离心率为
,上顶点为B,离心率为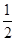 ,圆
,圆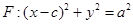 与
与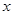 轴交于
轴交于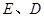 两点
两点 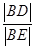 的值;
的值;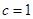 ,过点
,过点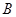 与圆
与圆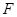 相切的直线
相切的直线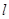 与
与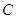 的另一交点为
的另一交点为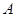 ,求
,求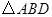 的面积
的面积 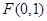 且与直线
且与直线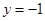 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为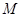 .点
.点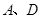 在轨迹
在轨迹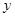 轴对称,过线段
轴对称,过线段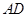 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线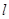 ,使直线
,使直线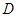 处的切线平行,设直线
处的切线平行,设直线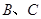 .
. ;
; 的距离等于
的距离等于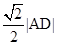 ,且
,且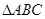 的面积为20,求直线
的面积为20,求直线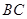 的方程.
的方程.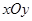 中,点
中,点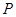 到两点
到两点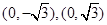 的距离之和等于4,设点
的距离之和等于4,设点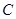 ,直线
,直线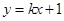 与
与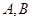 两点.
两点.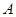 在第一象限,证明当
在第一象限,证明当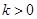 时,恒有
时,恒有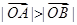 .
.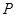 :
: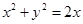 及抛物线
及抛物线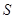 :
: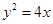 ,过圆心
,过圆心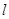 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为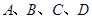 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线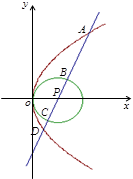
 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为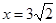 ,离心率为
,离心率为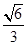 .若直线
.若直线 与椭圆
与椭圆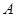 、
、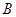 ,以线段
,以线段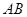 为直径作圆
为直径作圆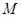 .
.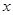 轴相切,求圆
轴相切,求圆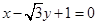 截得的线段长.
截得的线段长.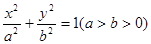 的离心率为
的离心率为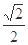 ,
,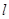 :y=x+2与原点为圆心,以椭圆C的短轴长为直
:y=x+2与原点为圆心,以椭圆C的短轴长为直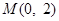 的直线
的直线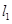 与椭圆
与椭圆 交于
交于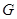 ,
,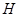 两点.设直线
两点.设直线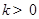 ,在
,在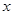 轴上是否存在点
轴上是否存在点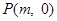 ,使得
,使得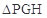 是以GH为底边的等腰三角形. 如果存在,求出实数
是以GH为底边的等腰三角形. 如果存在,求出实数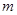 的取值范围,如果不存在,请说明理由.
的取值范围,如果不存在,请说明理由.