题目内容
给定圆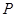 :
: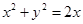 及抛物线
及抛物线 :
: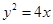 ,过圆心
,过圆心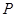 作直线
作直线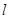 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为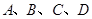 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线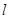 的方程.
的方程.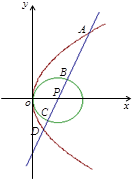
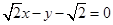 或
或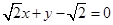 .
.
解析试题分析:本题考查圆、直线、抛物线相交的问题,考查学生分析问题解决问题的能力.先将圆的直径求出来,再设出直线方程,方程中的中有一个参数 ,本题的关键是解出
,本题的关键是解出 的值,将直线方程代入抛物线方程中,消去
的值,将直线方程代入抛物线方程中,消去 ,求
,求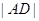 的长,再利用等差中项列出线段
的长,再利用等差中项列出线段 的关系,进而求出
的关系,进而求出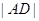 的长,与上面的
的长,与上面的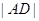 联立就可求出
联立就可求出 .
.
试题解析:圆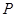 的方程为
的方程为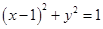 ,则其直径长
,则其直径长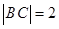 ,圆心为
,圆心为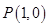 ,设
,设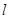 的方程为
的方程为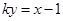 ,即
,即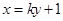 ,代入抛物线方程得:
,代入抛物线方程得: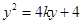 ,设
,设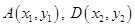 ,有
,有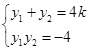 ,
,
则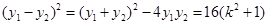 .
.
故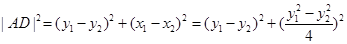
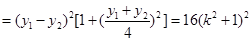 ,
,
因此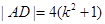 . 8分
. 8分
据等差,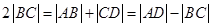 ,
,
所以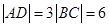 ,即
,即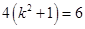 ,
,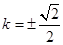 , 14分
, 14分
即: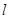 方程为
方程为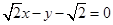 或
或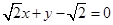 . 16分
. 16分
考点:1.等差数列中等差中项的概念;2.圆的半径;3.直线与抛物线的交点.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
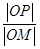 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.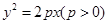 的准线过椭圆N:
的准线过椭圆N: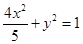 的左焦点,以坐标原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B,直线AB与x轴相交于点C.
的左焦点,以坐标原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B,直线AB与x轴相交于点C.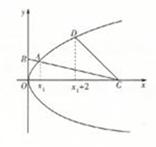
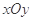 中,动点
中,动点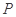 到两点
到两点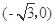 ,
,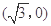 的距离之和等于
的距离之和等于 ,设点
,设点 ,直线
,直线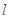 过点
过点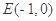 且与曲线
且与曲线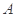 ,
,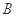 两点.
两点.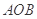 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△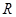 :
: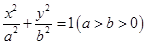 的长轴长为4,且过点
的长轴长为4,且过点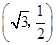 .
.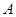 、
、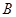 、
、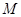 是椭圆上的三点,若
是椭圆上的三点,若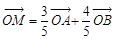 ,点
,点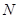 为线段
为线段 的中点,
的中点, 、
、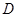 两点的坐标分别为
两点的坐标分别为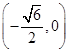 、
、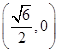 ,求证:
,求证: .
.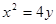 的焦点为
的焦点为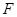 ,过
,过 (
(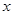 轴不平行)交抛物线分别于
轴不平行)交抛物线分别于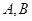 两点,点
两点,点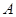 关于
关于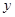 轴对称点为
轴对称点为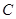 ,
,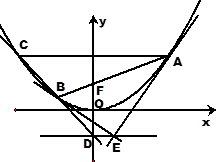
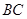 与
与 必为定点;
必为定点;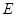 ,求
,求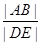 的最小值,并求当
的最小值,并求当 轴上,且过点
轴上,且过点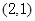 .
.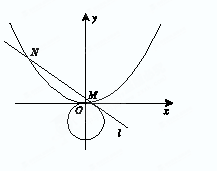
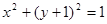 相切的直线
相切的直线 交抛物线于不同的两点
交抛物线于不同的两点 若抛物线上一点
若抛物线上一点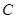 满足
满足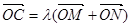
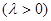 ,求
,求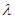 的取值范围.
的取值范围.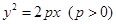 与直线
与直线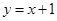 相切,
相切,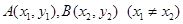 是抛物线上两个动点,
是抛物线上两个动点, 为抛物线的焦点,
为抛物线的焦点, 的垂直平分线
的垂直平分线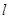 与
与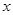 轴交于点
轴交于点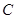 ,且
,且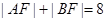 .
.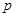 的值;
的值;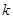 的取值范围.
的取值范围.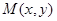 与定点
与定点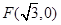 的距离和它到直线
的距离和它到直线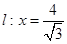 的距离之比是常数
的距离之比是常数 ,记
,记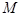 的轨迹为曲线
的轨迹为曲线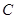 .
.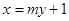 与曲线
与曲线 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为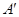 ,试问:当
,试问:当 变化时,直线
变化时,直线 与
与