题目内容
设抛物线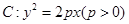 的焦点为
的焦点为 ,准线为
,准线为 ,
,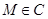 ,以
,以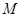 为圆心的圆
为圆心的圆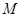 与
与 相切于点
相切于点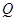 ,
,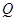 的纵坐标为
的纵坐标为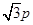 ,
,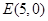 是圆
是圆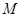 与
与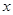 轴除
轴除 外的另一个交点.
外的另一个交点.
(I)求抛物线 与圆
与圆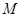 的方程;
的方程;
(II)过 且斜率为
且斜率为 的直线
的直线 与
与 交于
交于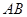 两点,求
两点,求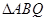 的面积.
的面积.
(I)抛物线为: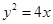 ,圆的方程为:
,圆的方程为: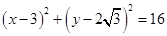 ;( II)
;( II)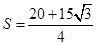 .
.
解析试题分析:(I)根据抛物线的方程与准线,可得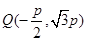 ,由
,由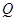 的纵坐标为
的纵坐标为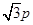 ,
,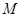 的纵坐标为
的纵坐标为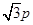 ,即
,即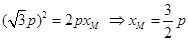 ,则
,则 ,由题意可知:
,由题意可知: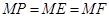 ,则在等腰三角形中有
,则在等腰三角形中有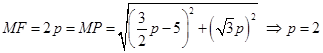 或
或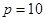 ,由于
,由于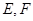 不重合,则
不重合,则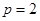 .则抛物线与圆的方程就得出.
.则抛物线与圆的方程就得出.
(II)对于圆锥曲线中求面积题目,第一求出弦长,第二求出点到直线距离即可,根据题意可写出直线方程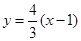 ,联立
,联立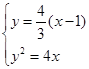 得
得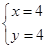 或
或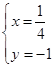 ,则
,则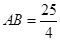 ,由点到直线距离得
,由点到直线距离得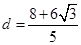 即
即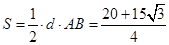 .
.
试题解析:(I)根据抛物线的定义:有 由
由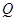 的纵坐标为
的纵坐标为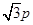 ,
,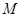 的纵坐标为
的纵坐标为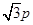
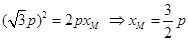 ,
, ,则
,则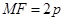 ,又由
,又由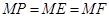 得
得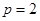 ,
,
则抛物线为: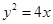 ,圆的方程为:
,圆的方程为: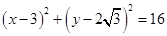
(II) 根据题意可写出直线方程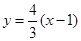 ,联立
,联立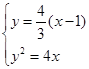 得
得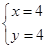 或
或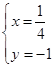 ,则
,则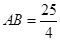 ,
,
由点到直线距离得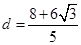 即
即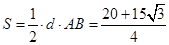 .
.
考点:1.抛物线定义以及抛物线与直线间的关系,2.求面积问题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
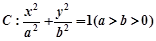 的焦点为
的焦点为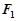
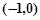 ,
,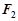
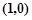 ,且经过点
,且经过点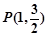 .
. 的方程;
的方程; 与椭圆
与椭圆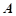 、
、 两点,问在椭圆
两点,问在椭圆 ,使四边形
,使四边形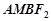 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线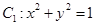 在矩阵
在矩阵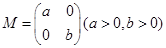 的变换作用下得到曲线
的变换作用下得到曲线 .
.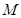 ;
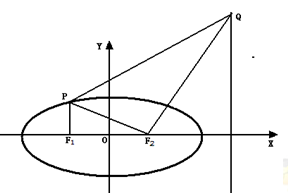
;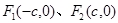 分别是椭圆C:
分别是椭圆C: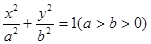 的左、右焦点,过点
的左、右焦点,过点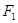 作
作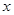 轴的垂线,交椭圆
轴的垂线,交椭圆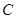 的上半部分于点
的上半部分于点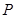 ,过点
,过点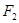 作
作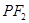 的垂线交直线
的垂线交直线 于点
于点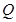 .
.
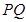 与椭圆
与椭圆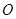 ,半径为
,半径为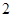 .从这个圆上任意一点
.从这个圆上任意一点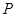 向
向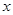 轴作垂线
轴作垂线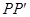 ,
,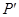 为垂足.
为垂足.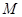 的轨迹方程;
的轨迹方程; 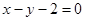 与
与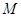 的轨迹相交于
的轨迹相交于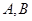 两点,求
两点,求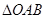 的面积
的面积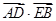 的最小值.
的最小值.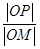 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线. 焦点在x轴上,左、右焦眯分别为F1,F2,且|F1F2|=2,点P(1,
焦点在x轴上,左、右焦眯分别为F1,F2,且|F1F2|=2,点P(1,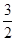 )在椭圆C上.
)在椭圆C上.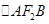 的面积为
的面积为 ,求直线l的方程.
,求直线l的方程.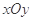 中,动点
中,动点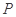 到两点
到两点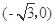 ,
,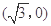 的距离之和等于
的距离之和等于 ,设点
,设点 ,直线
,直线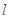 过点
过点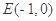 且与曲线
且与曲线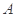 ,
,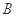 两点.
两点.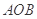 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△