题目内容
【题目】已知AB是平面内一条长度为4的线段，P是平面内一动点，P可以与A，B重合.当P与A，B不重合时，直线PA与PB的斜率之积为
，
（1）建立适当的坐标系，求动点P的轨迹方程；
（2）一个矩形的四条边与（1）中的轨迹M均相切，求该矩形面积的范围.
【答案】（1）以AB中点为坐标原点，以AB为x轴建立坐标系，
（2）
【解析】
（1））以AB中点为坐标原点，以AB为x轴建立坐标系，设
，把已知用坐标表示可得轨迹方程；
（2）矩形一边斜率不存在时直接求出面积，斜率存在时，设一边所在的直线为
，则对边为
，另一边所在的直线为
，则对边为
，由直线与圆相切得
和
的关系式，由平行间距离公式求得矩形的两边长，计算面积为
的函数，由函数单调性得取值范围．
（1）以AB中点为坐标原点，以AB为x轴建立坐标系，
则
，
，设，当P与A，B不重合时，
，
，
，
P可以与A，B重合，所以P的轨迹方程为；
（2）矩形的各边与椭圆相切，记矩形面积为S，
当矩形的一条边与坐标轴平行时易知
，
当矩形各边均不与坐标轴平行时，根据对称性，
设其中一边所在的直线为，则对边为，
另一边所在的直线为，则对边为，
，
，
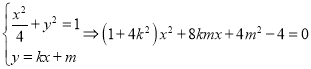则矩形的一边长
，
同理可得：
，矩形的另一边长，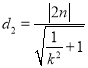
，
，
，
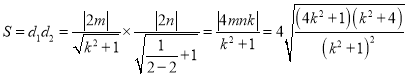
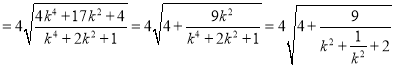
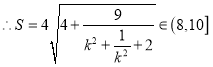综上：
.
练习册系列答案
相关题目
