题目内容
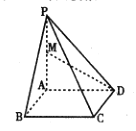
【题目】已知A,B,C是抛物线W:y2=4x上的三个点,D是x轴上一点.
(1)当点B是W的顶点,且四边形ABCD为正方形时,求此正方形的面积;
(2)当点B不是W的顶点时,判断四边形ABCD是否可能为正方形,并说明理由.
【答案】(1)32;(2)不可能,理由见解析.
【解析】
(1)根据正方形的性质知![]() 的坐标为
的坐标为![]() ,代入抛物线方程,解出
,代入抛物线方程,解出![]() ,即可得到正方形的面积;
,即可得到正方形的面积;
(2)先假设四边形![]() 为正方形,设直线
为正方形,设直线![]() 的方程为
的方程为![]() ,曲直联立,得到韦达定理,并依次求得
,曲直联立,得到韦达定理,并依次求得![]() 中点
中点![]() 坐标、弦长
坐标、弦长![]() 以及点
以及点![]() 的坐标和弦长
的坐标和弦长![]() ,再利用
,再利用![]() ,得到
,得到![]() 与
与![]() 等量关系①,然后利用
等量关系①,然后利用![]() ,得到
,得到![]() 与
与![]() 等量关系②,联立①②即可判定四边形
等量关系②,联立①②即可判定四边形![]() 是否可能为正方形.
是否可能为正方形.
(1)当点![]() 是
是![]() 的顶点时,设
的顶点时,设![]() 与
与![]() 相交于点
相交于点![]() ,则
,则![]() ,
,
假设点![]() 在
在![]() 轴上方,则
轴上方,则![]() 的坐标为
的坐标为![]() ,
,
代入抛物线方程得![]() ,此时正方形的边长为
,此时正方形的边长为![]() ,
,
所以正方形的面积为![]() .
.
(2)四边形![]() 不可能为正方形.
不可能为正方形.
当点![]() 不是
不是![]() 的顶点时,直线
的顶点时,直线![]() 的斜率一定存在,设其方程为
的斜率一定存在,设其方程为![]() ,
,
![]() 、
、![]() 坐标分别为
坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立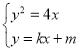 ,则
,则![]() ,
,
所以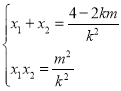 ,
,![]() ,
,
因此,![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
若四边形![]() 为正方形,则
为正方形,则![]() 的中点也是
的中点也是![]() ,
,![]() ,
,
因为点![]() 在
在![]() 轴上,所以
轴上,所以![]() ,所以
,所以![]() ,
,
代入![]() ,得
,得![]() ,即
,即![]() ,
,
所以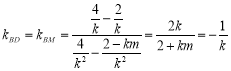 ,
,
化简得![]() ,①
,①
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
化简得![]() ,②
,②
由①②得,![]() ,
,![]() 无解,
无解,
故四边形![]() 不可能为正方形.
不可能为正方形.

练习册系列答案
相关题目