题目内容
【题目】已知函数![]() ,其函数图象的相邻两条对称轴之间的距离为
,其函数图象的相邻两条对称轴之间的距离为![]() .
.
(1)求函数![]() 的解析式及对称中心;
的解析式及对称中心;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)将函数化为![]() 后再求对称中心.(2)由题意得
后再求对称中心.(2)由题意得![]() ,且
,且![]() ,令
,令![]() 后可将问题转化为关于
后可将问题转化为关于![]() 的方程
的方程![]() 在区间
在区间![]() 上仅有一个实数根求解,然后根据方程根的分布可得所求结果.
上仅有一个实数根求解,然后根据方程根的分布可得所求结果.
详解:(1)由题意得![]()
![]()
![]()
![]() .
.
∵函数图象的相邻两条对称轴之间的距离为![]() ,
,
∴![]() ,
,
∴![]()
![]() sin(
sin(![]() )
)![]()
由![]() ,
,
得![]() ,
,
![]() .
.
(2)由题意知![]() ,
,
∵![]() ,
,
∴![]() .
.
设![]() .
.
∵关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,
上有两个不相等的实根,
∴关于![]() 的方程
的方程![]() 在区间
在区间![]() 上仅有一个实数根.
上仅有一个实数根.
令H(t)=![]() ,
, ![]() ,
,
则函数H(t)的图象为开口向上的抛物线,且过定点(0,2).
故由条件可得H(![]() )=9+
)=9+ ,
,
解得![]() ,
,
∴实数![]() 的取值范围为
的取值范围为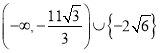 .
.

练习册系列答案
相关题目
【题目】某企业准备投资 ![]() 万元兴办一所中学,对当地教育市场进行调查后,得到了如下的数据表格(以班级为单位):
万元兴办一所中学,对当地教育市场进行调查后,得到了如下的数据表格(以班级为单位):
|
| |
初中 | 26 | 4 |
高中 | 54 | 6 |
第一年因生源和环境等因素,全校总班级至少 ![]() 个,至多
个,至多 ![]() 个,若每开设一个初、高中班,可分别获得年利润
个,若每开设一个初、高中班,可分别获得年利润 ![]() 万元、
万元、 ![]() 万元,则第一年利润最大为
万元,则第一年利润最大为 ![]()
A. ![]() 万元 B.
万元 B. ![]() 万元 C.
万元 C. ![]() 万元 D.
万元 D. ![]() 万元
万元


