题目内容
圆M:x2+y2-4x-2y+4=0(1)若圆M的切线在x轴上的截距是y轴上的截距的2倍,求切线的方程;
(2)从圆外一点P(a,b),向该圆引切线PA,切点为A,且PA=PO,O为坐标原点,求证:以PM为直径的圆过异于M的定点,并求该定点的坐标
分析:①首先对切线分两种情况讨论,过原点时与不过原点时.然后分别设出直线,根据切线在x轴上的截距是y轴上的截距的2倍建立等式,分别求出切线方程.
②根据PA2=PO2,得到a,b的关系式2a+b=2,然后表示出以PM为直径的圆方程.通过对该圆的方程的分析,求出其通过的定点即可.
②根据PA2=PO2,得到a,b的关系式2a+b=2,然后表示出以PM为直径的圆方程.通过对该圆的方程的分析,求出其通过的定点即可.
解答:解:(1)当切线过原点时,设切线为y=kx,
由
=1
得k=
,k=0(舍)
当切线不过原点时,
设切线为
+
=1
即x+2y=2a,
由
=1
得2a=4±
6′,
所以所求的切线方程为y=
x,x+2y=4±
(2)由条件PA2=PO2,
得(a-2)2+(b-1)2=a2+b2
得2a+b=2
以PM为直径的圆方程为x2+y2-(2+a)x-(b+1)y+b+2a=0
12′x2+y2-(2+a)x-(3-2a)y+2=0
所以异于M的定点为(
,
)
由
| |2k-1| | ||
|
得k=
| 4 |
| 3 |
当切线不过原点时,
设切线为
| x |
| 2a |
| y |
| a |
即x+2y=2a,
由
| |2+2-2a| | ||
|
得2a=4±
| 5 |
所以所求的切线方程为y=
| 4 |
| 3 |
| 5 |
(2)由条件PA2=PO2,
得(a-2)2+(b-1)2=a2+b2
得2a+b=2
以PM为直径的圆方程为x2+y2-(2+a)x-(b+1)y+b+2a=0
12′x2+y2-(2+a)x-(3-2a)y+2=0
|
|
|
所以异于M的定点为(
| 4 |
| 5 |
| 2 |
| 5 |
点评:本题考查直线与圆的位置关系-相切,以及当直线与圆相切时的性质.通过两个小题不同的条件分别分析求解.本题在考查性质的同时也考查了运算能力以及对题目整体的把握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
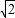 的概率为 .
的概率为 .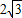 ,那么
,那么 的值等于 .
的值等于 .