Question

已知圆M：x²+y²=4，在圆M上随机取一点P，则P到直线x+y=2的距离大于2

2

的概率为

1

4

．

Answer 1

分析：利用点到直线的距离公式求出满足条件的点的弧长、几何概型的计算公式即可得出．

解答：解：由点到直线的距离公式得点O到直线x+y=2的距离为

|-2|

2

=

2

，
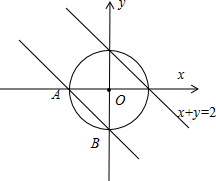
故到直线x+y=2距离为2

2

的点在直线x+y=2关于原点对称的直线AB：x+y+2=0上，
满足P到直线x+y=2的距离大于2

2

的点位于劣弧AB上，且∠AOB=90°．
故概率P=

1

4

．
故答案为

1

4

．

点评：熟练掌握点到直线的距离公式及几何概型的计算公式是解题的关键．