题目内容
【题目】设函数![]() 是奇函数
是奇函数![]() 的导函数,
的导函数,![]() ,当
,当![]() 时,
时,![]() ,则使得
,则使得![]() 成立的
成立的![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
由已知当x>0时总有xf′(x)﹣f(x)<0成立,可判断函数g(x)![]() 为减函数,由已知f(x)是定义在R上的奇函数,可证明g(x)为(﹣∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,大致画出g(x)的图象,而不等式f(x)>0等价于xg(x)>0,数形结合解不等式组即可.
为减函数,由已知f(x)是定义在R上的奇函数,可证明g(x)为(﹣∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,大致画出g(x)的图象,而不等式f(x)>0等价于xg(x)>0,数形结合解不等式组即可.
设g(x)![]() ,则g(x)的导数为:g′(x)
,则g(x)的导数为:g′(x)![]() ,
,
∵当x>0时总有xf′(x)<f(x)成立,
即当x>0时,g′(x)恒小于0,
∴当x>0时,函数g(x)![]() 为减函数,
为减函数,
又∵g(﹣x)![]() g(x),
g(x),
∴函数g(x)为定义域上的偶函数
又∵g(﹣1)![]() 0,
0,
∴函数g(x)的图象大致如图:
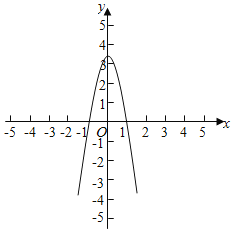
数形结合可得,不等式f(x)>0xg(x)>0
![]() 或
或![]() ,
,
0<x<1或x<﹣1.
故选:B.

练习册系列答案
相关题目