题目内容
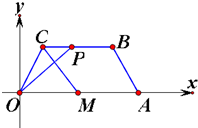
在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,A(6,0),C(1,
),点,M满足
=
,点P在线段BC上运动(包括端点),如图.
(1)求∠OCM的余弦值;
(2)是否存在实数λ,使(
-λ
)⊥
,若存在,求出满足条件的实数λ的取值范围,若不存在,请说明理由.
| 3 |
| OM |
| 1 |
| 2 |
| OA |
(1)求∠OCM的余弦值;
(2)是否存在实数λ,使(
| OA |
| OP |
| CM |

(1)由题意可得
=(6,0),
=(1,
),
=
=(3,0),
=(2,-
),
=(-1,-
),
故cos∠OCM=cos<
,
>=
=
.
(2)设P(t,
),其中1≤t≤5,λ
=(λt,
λ),
-λ
=(6-λt,-
λ),
=(2,-
).
若(
-λ
)⊥
,
则(
-λ
)•
=0,
即12-2λt+3λ=0,
可得(2t-3)λ=12.
若t=
,则λ不存在,
若t≠
,则λ=
,
∵t∈[1,
)∪(
,5],
故λ∈(-∞,-12]∪[
,+∞).
| OA |
| OC |
| 3 |
| OM |
| 1 |
| 2 |
| OA |
| CM |
| 3 |
| CO |
| 3 |
故cos∠OCM=cos<
| CO |
| CM |
| ||||
|
|
| ||
| 14 |
(2)设P(t,
| 3 |
| OP |
| 3 |
| OA |
| OP |
| 3 |
| CM |
| 3 |
若(
| OA |
| OP |
| CM |
则(
| OA |
| OP |
| CM |
即12-2λt+3λ=0,
可得(2t-3)λ=12.
若t=
| 3 |
| 2 |
若t≠
| 3 |
| 2 |
| 12 |
| 2t-3 |
∵t∈[1,
| 3 |
| 2 |
| 3 |
| 2 |
故λ∈(-∞,-12]∪[
| 12 |
| 7 |

练习册系列答案
相关题目
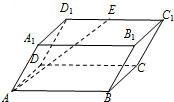
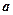 与
与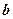 的夹角为
的夹角为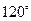 ,且
,且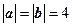 ,那么
,那么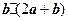 的值为 .
的值为 .