题目内容
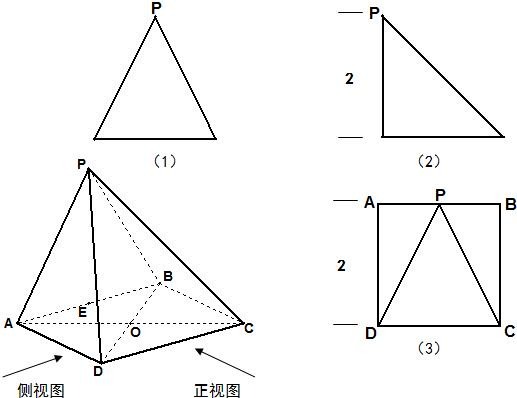
如图四棱锥P-ABCD,它的正视图如图(1),是等腰三角形,侧视图如图(2),是等腰直角三角形,俯视图如图(3),是正方形ABCD.
各长度如图所示.
(I)求证:平面ADP⊥平面ABP;
(II)设E为AB中点,试在线段PE上确定一点M,使得OM∥平面PDC,并证明;
(III)求四棱锥P-ABCD的体积.
分析:(1)由面面垂直证明线面垂直,再由线面垂直证明面面垂直.
(2)取线段PE的中点为M.由三角形中位线性质证明线线平行,从而证明线面平行.
(3)直接使用棱锥的体积公式,底面是边长为2的正方形,棱锥的高是2.
(2)取线段PE的中点为M.由三角形中位线性质证明线线平行,从而证明线面平行.
(3)直接使用棱锥的体积公式,底面是边长为2的正方形,棱锥的高是2.
解答:(1)证明:∵面ABP⊥面ABCD,AD⊥AB
∴AD⊥面ABP(2分)
∴平面ADP⊥平面ABP(3分)
(也可在此问中取AB中点E,只需证明AD与AB和PE垂直.)
(2)取线段PE的中点为M.(4分)
证明:延长EO至F,且F∈CD,连接PF.
在三角形EPF中,EM=MP,EO=OF,
∴MO∥PF(6分)
∵MO?面PDC(7分)
MO∥面PDC(8分)
(3)V=
Sh=
*4*2=
(13分)
∴AD⊥面ABP(2分)
∴平面ADP⊥平面ABP(3分)
(也可在此问中取AB中点E,只需证明AD与AB和PE垂直.)
(2)取线段PE的中点为M.(4分)
证明:延长EO至F,且F∈CD,连接PF.
在三角形EPF中,EM=MP,EO=OF,
∴MO∥PF(6分)
∵MO?面PDC(7分)
MO∥面PDC(8分)
(3)V=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
点评:本题考查线面平行、面面垂直的判定,椎体的体积.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且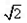 ,F是BC的中点.
,F是BC的中点.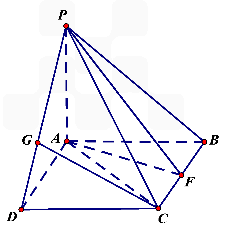
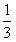 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点. 的值。
的值。 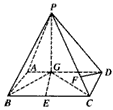
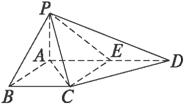
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.