题目内容
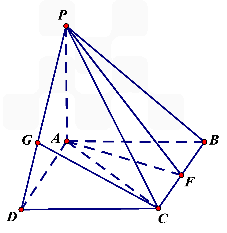
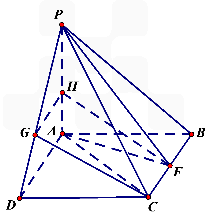
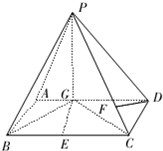
如图四棱锥P-ABCD中,底面ABCD是平行四边形,∠ABC=90°,PA⊥平面ABCD,PA=BC=1,AB=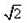 ,F是BC的中点.
,F是BC的中点.
(1)求证:DA⊥平面PAC;
(2)试在线段PD上确定一点G,使CG∥平面PAF,并求三棱锥A-CDG的体积.
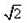 ,F是BC的中点.
,F是BC的中点.(1)求证:DA⊥平面PAC;
(2)试在线段PD上确定一点G,使CG∥平面PAF,并求三棱锥A-CDG的体积.
解:(1)证明:∵四边形是平行四边形,∴∠ACB=∠DAC=90°,
∵PA⊥平面ABCD∴PA⊥DA,
又AC⊥DA,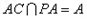 ,
,
∴DA⊥平面PAC
(2)设PD的中点为G,在平面PAD内作GH⊥PA于H,
则GH平行且等于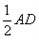 ,连接FH,则四边形FCGH为平行四边形
,连接FH,则四边形FCGH为平行四边形
∴GC∥FH,
∵FH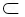 平面PAE,CG
平面PAE,CG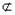 平面PAE,
平面PAE,
∴CG∥平面PAE,
∴G为PD中点时,CG∥平面PAE
设S为AD的中点,连结GS,则GS平行且等于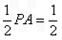
∵PA⊥平面ABCD
∴GS⊥平面ABCD
∴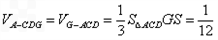
∵PA⊥平面ABCD∴PA⊥DA,
又AC⊥DA,
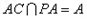 ,
,∴DA⊥平面PAC
(2)设PD的中点为G,在平面PAD内作GH⊥PA于H,
则GH平行且等于
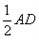 ,连接FH,则四边形FCGH为平行四边形
,连接FH,则四边形FCGH为平行四边形∴GC∥FH,
∵FH
 平面PAE,CG
平面PAE,CG 平面PAE,
平面PAE,∴CG∥平面PAE,
∴G为PD中点时,CG∥平面PAE
设S为AD的中点,连结GS,则GS平行且等于
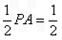
∵PA⊥平面ABCD
∴GS⊥平面ABCD
∴
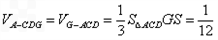


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且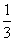 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.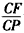 的值。
的值。 
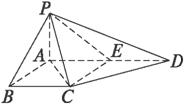
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.