题目内容
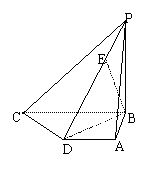
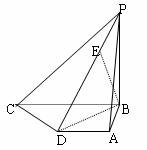
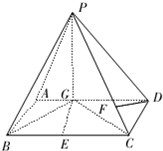 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且AG=
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且AG=| 1 |
| 3 |
(1)求证:PC⊥BG;
(2)求异面直线GE与PC所成角的余弦值;
(3)若F是PC上一点,且DF⊥GC,求
| CF |
| CP |
分析:(1)由已知PG⊥底面ABCD,可得PG⊥BG,结合BG⊥CG,可证得BG⊥面PGC,从而有PC⊥BG;
(2)以G为坐标原点,如图建立空间直角坐标系,求得
,
的坐标,利用向量的夹角公式即可求得异面直线GE与PC所成角的余弦值;
(3)设CF=λCP,求得点F与点D的坐标,从而得到
、
的坐标,由DF⊥GC即可求得
的值.
(2)以G为坐标原点,如图建立空间直角坐标系,求得
| GE |
| PC |
(3)设CF=λCP,求得点F与点D的坐标,从而得到
| DF |
| GC |
| CF |
| CP |
解答: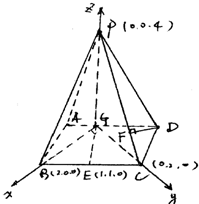 证明:(1)因为PG⊥底面ABCD,
证明:(1)因为PG⊥底面ABCD,
所以 PG⊥BG,又BG⊥CG,所以BG⊥面PGC,
所以PC⊥BG. (4分)
(2)建立如图空间直角坐标系,各点坐标如图所示,
=(1,1,0),
=(0,2,-4)
∴|cos<
,
>|=|
|=
. (8分)
(3)设CF=λCP,
则点F(0,2-2λ,4λ),又D(-
,
,0),
∴
=(
,
-2λ,4λ),
=(0,2,0),
由DF⊥GC得
•
=0,
∴2(
-2λ)=0.
得λ=
,
∴
=
(14分)
 证明:(1)因为PG⊥底面ABCD,
证明:(1)因为PG⊥底面ABCD,所以 PG⊥BG,又BG⊥CG,所以BG⊥面PGC,
所以PC⊥BG. (4分)
(2)建立如图空间直角坐标系,各点坐标如图所示,
| GE |
| PC |
∴|cos<
| GE |
| PC |
| ||||
|
|
| ||
| 10 |
(3)设CF=λCP,
则点F(0,2-2λ,4λ),又D(-
| 3 |
| 2 |
| 3 |
| 2 |
∴
| DF |
| 3 |
| 2 |
| 1 |
| 2 |
| GC |
由DF⊥GC得
| DF |
| GC |
∴2(
| 1 |
| 2 |
得λ=
| 1 |
| 4 |
∴
| CF |
| CP |
| 1 |
| 4 |
点评:本题异面直线及其所成的角,着重考查空间向量的坐标运算在空间几何中的作用,考查分析转化与数形结合的数学思想,属于难题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
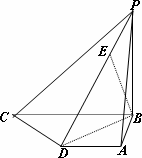

 (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD; (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD;