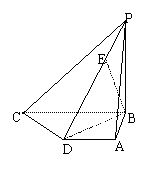
题目内容
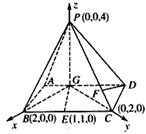
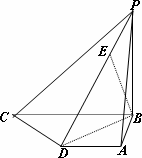
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且AG=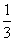 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
(Ⅰ)求证:PC⊥BG;
(Ⅱ)求异面直线GE与PC所成角的余弦值;
(Ⅲ)若F是PC上一点,且DF⊥GC,求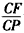 的值。
的值。
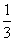 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.(Ⅰ)求证:PC⊥BG;
(Ⅱ)求异面直线GE与PC所成角的余弦值;
(Ⅲ)若F是PC上一点,且DF⊥GC,求
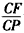 的值。
的值。 
| (Ⅰ)证明:因为PG⊥平面ABC, 所以PG⊥BC, 又BG⊥CG, 所以BG⊥面PCG, 所以PC⊥BG。 |
|
(Ⅱ)解:建立如图所示的空间直角坐标系,各点坐标如图所示,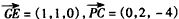 , ,∴ 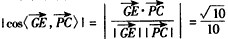 。 。(Ⅲ)设 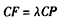 , ,则点 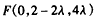 , ,又 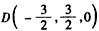 , ,∴  , ,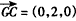 , ,由DF⊥DC,得 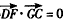 , ,∴ 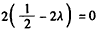 ,解得: ,解得: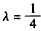 , ,∴ 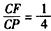 。 。 |
 |

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目

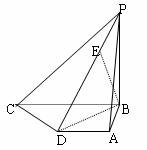 (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD; (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD;