题目内容
(本题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
市工商局于今年3月份,对市内流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的 饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
(Ⅰ)甲喝两瓶 饮料,均合格的概率
饮料,均合格的概率
(Ⅱ)甲、乙、丙每人喝两瓶,恰有一人喝到不合格饮料的概率(精确到0.01)
市工商局于今年3月份,对市内流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的
 饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求(Ⅰ)甲喝两瓶
 饮料,均合格的概率
饮料,均合格的概率(Ⅱ)甲、乙、丙每人喝两瓶,恰有一人喝到不合格饮料的概率(精确到0.01)
解:(Ⅰ)记“第一瓶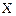 饮料合格”为事件
饮料合格”为事件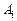 ,“第二瓶
,“第二瓶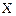 饮料合格”为事件
饮料合格”为事件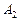 ,
,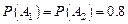 ,
,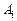 与
与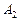 是相互独立事件,
是相互独立事件,
则“甲喝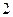 瓶
瓶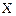 饮料都合格就是事件
饮料都合格就是事件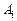 、
、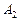 同时发生,根据相互独立事件的概率乘法公式得:
同时发生,根据相互独立事件的概率乘法公式得: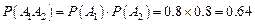 ………6分
………6分
(Ⅱ)记“一人喝到合格的2瓶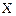 饮料”为事件
饮料”为事件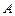 ,“三人每人喝2瓶
,“三人每人喝2瓶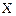 饮料只有一人喝到不合格饮料”相当于进行3次独立重复试验,事件
饮料只有一人喝到不合格饮料”相当于进行3次独立重复试验,事件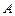 发生两次.
发生两次.
根据n次独立重复试验中事件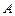 发生
发生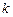 次的概率公式,3人喝6瓶
次的概率公式,3人喝6瓶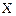 饮料只有1人喝到不合格的概率:
饮料只有1人喝到不合格的概率: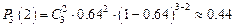
即甲、乙、丙3人中只有1人喝2瓶不合格的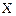 饮料的概率为0.44 ………13分
饮料的概率为0.44 ………13分
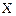 饮料合格”为事件
饮料合格”为事件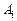 ,“第二瓶
,“第二瓶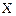 饮料合格”为事件
饮料合格”为事件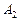 ,
,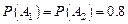 ,
,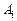 与
与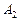 是相互独立事件,
是相互独立事件,则“甲喝
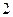 瓶
瓶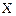 饮料都合格就是事件
饮料都合格就是事件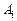 、
、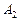 同时发生,根据相互独立事件的概率乘法公式得:
同时发生,根据相互独立事件的概率乘法公式得: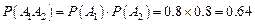 ………6分
………6分(Ⅱ)记“一人喝到合格的2瓶
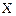 饮料”为事件
饮料”为事件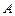 ,“三人每人喝2瓶
,“三人每人喝2瓶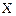 饮料只有一人喝到不合格饮料”相当于进行3次独立重复试验,事件
饮料只有一人喝到不合格饮料”相当于进行3次独立重复试验,事件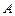 发生两次.
发生两次.根据n次独立重复试验中事件
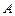 发生
发生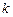 次的概率公式,3人喝6瓶
次的概率公式,3人喝6瓶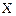 饮料只有1人喝到不合格的概率:
饮料只有1人喝到不合格的概率: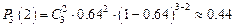
即甲、乙、丙3人中只有1人喝2瓶不合格的
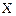 饮料的概率为0.44 ………13分
饮料的概率为0.44 ………13分略

练习册系列答案
相关题目
 ,设
,设 为这名学生在途中遇到的红灯次数,D
为这名学生在途中遇到的红灯次数,D 是甲抛掷一枚骰子(六个面分别标有1-6个点的正方体)得到的点数,则方程
是甲抛掷一枚骰子(六个面分别标有1-6个点的正方体)得到的点数,则方程 有两个不相等的实数根的概率为( )
有两个不相等的实数根的概率为( )


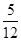
 ,点
,点 是圆内的任意一点,直线
是圆内的任意一点,直线 .
.  ;
;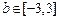 ,求直线
,求直线 与
与 圆
圆 相交的概率.
相交的概率. ”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:

 分别为2,3,4,5,现从中任取三条,则以这三条线段为边可以构成三角形的概率是 ▲
分别为2,3,4,5,现从中任取三条,则以这三条线段为边可以构成三角形的概率是 ▲