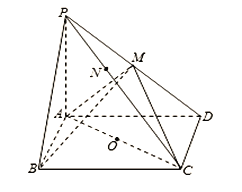
题目内容
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 的方程为
的方程为![]() ,左右焦点分别为
,左右焦点分别为![]() ,
,![]() ,
,![]() 为短轴的一个端点,且
为短轴的一个端点,且![]() 的面积为
的面积为![]() .设过原点的直线
.设过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的一点,且直线
的一点,且直线![]() ,
,![]() 的斜率都存在,
的斜率都存在,![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 为椭圆
为椭圆![]() 上位于
上位于![]() 轴上方的一点,且
轴上方的一点,且![]() 轴,
轴,![]() 、
、![]() 为曲线
为曲线![]() 上不同于
上不同于![]() 的两点,且
的两点,且![]() ,设直线
,设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)设点A(x1,y1)、P(x2,y2),则B(-x1,-y1),将点A、P的坐标代入椭圆C的方程,得出两个等式,将两等式相减,结合直线PA、PB的斜率之积,得出![]() =
=![]() ,再利用△RF1F2的面积为
,再利用△RF1F2的面积为![]() ,得出bc=
,得出bc=![]() ,联立两个方程,可求出a、b的值;
,联立两个方程,可求出a、b的值;
(2)设直线QM的斜率为k,结合已知条件得出直线QN的斜率为-k,将直线QM的方程与椭圆方程联立,求出点M的横坐标,利用-k代替k得出点N的横坐标,然后利用斜率公式得出直线MN的斜率为![]() ,于是得出直线MN的方程为y=
,于是得出直线MN的方程为y=![]() x+d,将直线MN的方程与椭圆C的方程联立,由△>0并结合点Q在直线MN的上方可得出d的取值范围.
x+d,将直线MN的方程与椭圆C的方程联立,由△>0并结合点Q在直线MN的上方可得出d的取值范围.
(1)解:设![]() ,
,![]() ,则
,则![]() ,
,
进一步得,![]() ,
,![]() ,
,
两个等式相减得,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
由![]() 的面积为
的面积为![]() 得,
得,![]() ,即
,即![]() ,
,
即![]() ,
,![]() ,所以
,所以![]() ,
,![]() ;
;
(2)设直线![]() 的斜率为
的斜率为![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() 关于直线
关于直线![]() 对称,
对称,
所以直线![]() 的斜率为
的斜率为![]() ,
,
算得![]() ,
,![]() ,
,
所以直线![]() 的方程是
的方程是![]() ,
,
设![]() ,
,![]()
由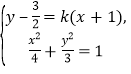 消去
消去![]() 得,
得,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
将上式中的![]() 换成
换成![]() 得,
得,![]() ,
,
所以![]()
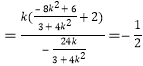 ,
,
所以直线![]() 的方程是
的方程是![]() ,
,
代入椭圆方程![]() 得,
得,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又因为![]() 在
在![]() 点下方,所以
点下方,所以![]() ,所以
,所以![]() .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目