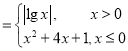Question

【题目】已知数列｛an｝的前n项和Sn=2an-2(n∈Z+).

（1）求通项公式an；

（2）设，为数列｛bn｝的前n项和，求正整数k，使得对任意的n∈Z+，均有T4≥Tn；

（3）设，Rn为数列{cn}的前n项和，若对任意的n∈Z+，均有Rn<λ，求λ的最小值.

Answer 1

【答案】(1) an =2n.(2) k=4.(3)

【解析】

（1）由Sn=2an-2，得5n+1=2n+1-2.

两式相减得an+1=2an+1-2anan+1=2an.

于是，{an}为等比数列，公比q=2.

由S1=2a1-2 a1=2al-2a1=2.

从而，an =2n.

（2）由（1）知

.

计算知b1=0，b2>0，b3>0，b4>0.

当n≥5时，由

，

知当n≥5时，为递减数列.

于是，n≥5时，

则n≥5时，

故T1<T2<T3<T4，T4>T5>….

从而，对任意的n∈Z+，均有T4≥Tn.因此，k=4.

（3）由（1）知

又对任意的n∈Z+，均有Rn<λ，知A≥.

从而，λ的最小值为.