题目内容
已知函数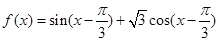 .
.
(Ⅰ)求函数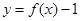 的单调递增区间;
的单调递增区间;
(Ⅱ)设函数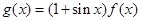 ,求
,求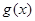 的值域.
的值域.
(Ⅰ)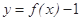 的单调增区间是
的单调增区间是 ;(Ⅱ)函数
;(Ⅱ)函数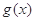 的值域为
的值域为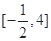 .
.
解析试题分析:(Ⅰ)由函数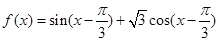 ,求函数
,求函数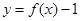 的单调递增区间,首先对
的单调递增区间,首先对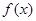 进行变化,可将
进行变化,可将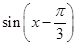 与
与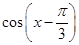 进行展开,也可利用
进行展开,也可利用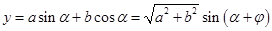 ,把
,把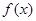 变成一个角的一个三角函数,利用
变成一个角的一个三角函数,利用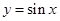 的单调递增区间,来求
的单调递增区间,来求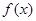 的单调递增区间,从而可得
的单调递增区间,从而可得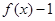 的单调递增区间;(Ⅱ)函数
的单调递增区间;(Ⅱ)函数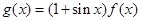 ,求
,求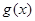 的值域,首先求出
的值域,首先求出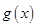 的解析式,
的解析式,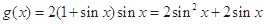 ,把它看做关于
,把它看做关于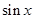 的二次函数,利用二次函数的单调性即可求出
的二次函数,利用二次函数的单调性即可求出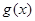 的值域.
的值域.
试题解析:(Ⅰ)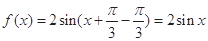 , 3分
, 3分 ,
,
∴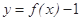 的单调增区间是
的单调增区间是 6分
6分
(Ⅱ)由(1)可得,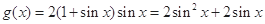 , 7分
, 7分
设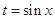 ,当
,当 时,
时,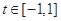 ,
,
则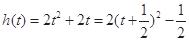 , 9分
, 9分
由二次函数的单调性可知, ,
,
又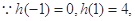
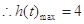 , 11分
, 11分
则函数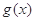 的值域为
的值域为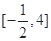 . 12分
. 12分
考点:三角恒等变化,三角函数的单调性,三角函数的值域.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
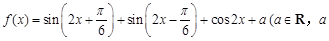 为常数).
为常数).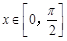 时,
时,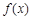 的最小值为
的最小值为 ,求a的值.
,求a的值.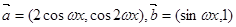 (
(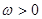 ),
),  ,且
,且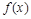 的周期为
的周期为 .
.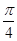 )的值;
)的值;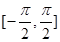 上的单调递增区间.
上的单调递增区间.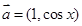 ,
,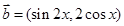 ,且
,且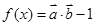
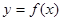
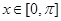 的单调增区间;
的单调增区间; 分别为角
分别为角 的对边,若
的对边,若 ,B=
,B=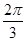 ,且
,且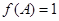 , 求三角形ABC的边
, 求三角形ABC的边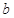 的值.
的值.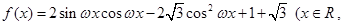
 >
> 的最小正周期是
的最小正周期是 .
. <
< 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.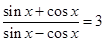 .
.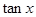 的值;
的值; 是第三象限的角,化简三角式
是第三象限的角,化简三角式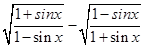 ,并求值.
,并求值.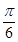 ]时,f(x)的最大值为2,求a的值.
]时,f(x)的最大值为2,求a的值.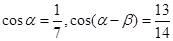 ,且
,且 .
. ;
;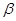 .
.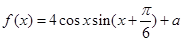 的最大值为2.
的最大值为2.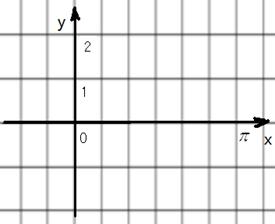
 的值及
的值及 的最小正周期;
的最小正周期; 上的图像.
上的图像.