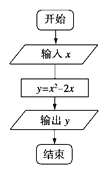
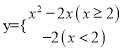题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(Ⅱ)若对![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)证明![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)详见解析.
;(III)详见解析.
【解析】试题分析:(1)运用导数与函数的单调性的关系等知识直接求解;(2)先对函数进行求导,再运用分类讨论的方法对不等式进行分析转化再运用导数知识求解;(3)先借助(1)的结论建立不等式,再运用叠加法、放缩法分析推证。
试题解析:
解:(Ⅰ)当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
∴函数![]() 的最大值
的最大值![]() .
.
(Ⅱ)![]() ,∵
,∵![]() ,∴
,∴![]() .
.
①当![]() 时,
时,![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上是减函数,∴
上是减函数,∴![]() 适合题意.
适合题意.
②当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() ,
,
不能使![]() 在
在![]() 恒成立.
恒成立.
③当![]() 时,
时,
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上为增函数,
上为增函数,
∴![]() ,不能使
,不能使![]() 在
在![]() 恒成立,
恒成立,
∴![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)由(Ⅰ)得![]() ,
,
∴![]() (
(![]() ),
),
取![]() ,
,
![]() ,则
,则![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目