Question

【题目】在极坐标系中，圆C的方程为ρ＝4cosθ，以极点为坐标原点，极轴为x轴的非负半轴建立平面直角坐标系，直线l经过点M（5，6），且斜率为．

（1）求圆 C的平面直角坐标方程和直线l的参数方程；

（2）若直线l与圆C交于A，B两点，求|MA|+|MB|的值．

Answer 1

【答案】（1）（x﹣2）2+y2＝4 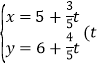为参数 ）； （2）.

【解析】

（1）由可求得圆的直角坐标方程，直线l经过点M（5，6），且斜率为，由直线的参数方程公式可得答案；

（2）把直线l的参数方程代入圆C, 得：5t2+66t+205＝0然后得出|MA|+|MB|的值.

（1）∵圆C的方程为ρ＝4cosθ，∴ρ2＝4ρcosθ，

∵ρ2＝x2+y2，ρcosθ＝x，

∴圆C的平面直角坐标方程为：（x﹣2）2+y2＝4，

∵直线l经过点M（5，6），且斜率为，

∴.

∴直线l的参数方程为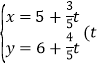为参数 ）．

（2）把直线l的参数方程代入圆C：（x﹣2）2+y2＝4，得：5t2+66t+205＝0，

所以