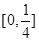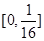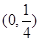题目内容
已知函数f(x)=|log2|x﹣1||,且关于x的方程[f(x)]2+af(x)+2b=0有6个不同的实数解,若最小的实数解为﹣1,则a+b的值为
| A.-2 | B.-1 | C.0 | D.1 |
B
解析试题分析:根据题意,由于函数f(x)=|log2|x﹣1||,且关于x的方程[f(x)]2+af(x)+2b=0有6个不同的实数解,解:作出函数f(x)=|log2|x-1||的图象,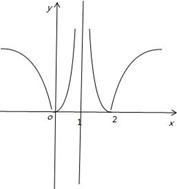
∵方程[f(x)]2+af(x)+2b=0有6个不同的实数解,∴如图所示:令t=f(x),方程[f(x)]2+af(x)+2b=0转化为:t2+at+2b=0则方程有一零根和一正根,又∵最小的实数解为-3∴f(-3)=1,∴方程:t2+at+2b=0的两根是0和2,由韦达定理得:a=-2,b=0,∴a+b=-2,故选B
考点:函数的与方程
点评:解决的关键是对于函数与方程的等价转化思想的运用,属于基础题。

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
设函数 为定义在
为定义在 上的奇函数,对任意
上的奇函数,对任意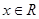 都有
都有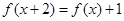 成立,则
成立,则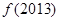 的值为( )
的值为( )
A.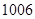 | B.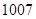 | C.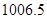 | D.无法确定 |
设函数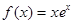 ,则( )
,则( )
A.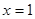 为 为 的极大值点 的极大值点 | B.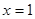 为 为 的极小值点 的极小值点 |
C. 为 为 的极大值点 的极大值点 | D. 为 为 的极小值点 的极小值点 |
下列4对函数中表示同一函数的是( )
A.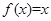 , , 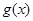 = =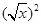 | B.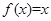 , ,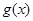  = = |
C. = =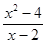 , ,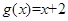 | D.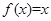 , , 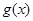 = =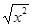 |
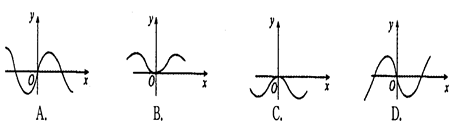
函数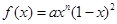 在区间〔0,1〕上的图像如图所示,则n可能是( )
在区间〔0,1〕上的图像如图所示,则n可能是( )
| A.1 | B.2 | C.3 | D.4 |
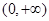 上的单调递减函数
上的单调递减函数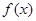 ,若
,若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )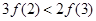
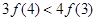
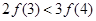
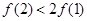
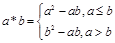 ,设
,设 ,且关于x的方程
,且关于x的方程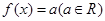 恰有三个互不相等的实数根,则实数
恰有三个互不相等的实数根,则实数 的取值范围是
的取值范围是