题目内容
设函数 为定义在
为定义在 上的奇函数,对任意
上的奇函数,对任意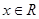 都有
都有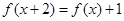 成立,则
成立,则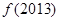 的值为( )
的值为( )
A.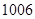 | B.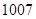 | C.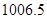 | D.无法确定 |
C
解析试题分析:因为,函数 为定义在
为定义在 上的奇函数,对任意
上的奇函数,对任意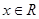 都有
都有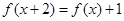 成立,所以,
成立,所以,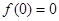 ,
,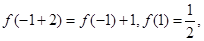
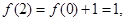
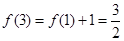 ,
,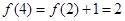 ,……由此归纳出
,……由此归纳出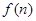 构成公差为
构成公差为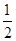 的等差数列,所以,
的等差数列,所以,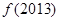 =
=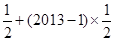 =
=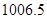 ,故选C。
,故选C。
考点:本题主要考查奇函数的性质,等差数列的通项公式,归纳推理。
点评:中档题,解答本题的关键是首先归纳得到对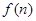 的认识,并利用等差数列知识进一步解题。
的认识,并利用等差数列知识进一步解题。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
函数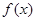 的定义域为开区间
的定义域为开区间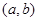 ,导函数
,导函数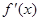 在
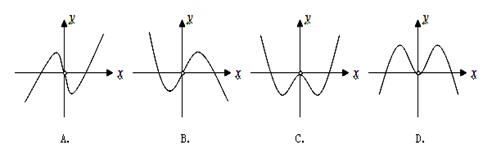
在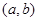 内的图象如图所示,则函数
内的图象如图所示,则函数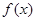 在开区间
在开区间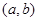 内有极大值( )
内有极大值( )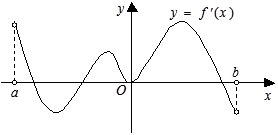
| A.1个 | B.4个 |
| C.3个 | D.2个 |
设偶函数 的定义域为R,当
的定义域为R,当 时,
时, 是增函数,则
是增函数,则
的大小关系是( )
A. > >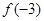 > >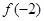 | B. > >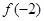 > >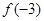 |
C. < <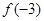 < <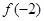 | D. < <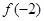 < <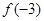 |
函数 的图象与直线
的图象与直线 的公共点数目是( )
的公共点数目是( )
A. | B. | C. 或 或 | D. 或 或 |
已知函数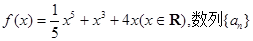 是等差数列,
是等差数列, 的值
的值
| A.恒为正数 | B.恒为负数 | C.恒为O | D.可正可负 |
 的一个根所在的区间是
的一个根所在的区间是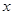
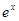
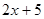
 B.
B.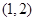 C.
C.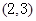 D.
D.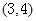
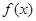 ,
,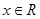 ,且
,且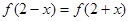 ,当
,当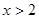 时,
时,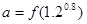 ,
,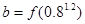 ,
,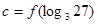 ,则
,则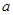 、
、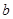 、
、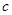 的大小顺序是( )。
的大小顺序是( )。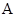 .
. 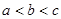
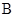 .
. 
 .
. 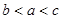
 .
.