题目内容
已知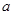 是实数,函数
是实数,函数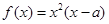 。
。
(Ⅰ)若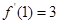 ,求
,求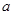 的值及曲线
的值及曲线 在点
在点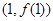 处的切线方程;
处的切线方程;
(Ⅱ)求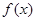 在区间
在区间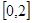 上的最大值。
上的最大值。
(1)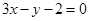 (2)
(2)
解析试题分析:(Ⅰ)解: ,
,
因为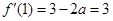 ,
,
所以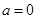 .
.
又当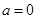 时,
时,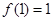 ,
,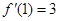 ,
,
所以曲线 在
在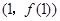 处的切线方程为
处的切线方程为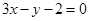 .
.
(Ⅱ)解:令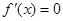 ,解得
,解得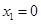 ,
,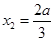 .
.
当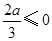 ,即
,即 时,
时,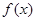 在
在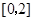 上单调递增,从而
上单调递增,从而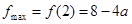 .
.
当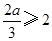 ,即
,即 时,
时,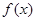 在
在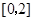 上单调递减,从而
上单调递减,从而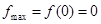 .
.
当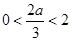 ,即
,即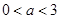 时,
时,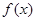 在
在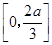 上单调递减,在
上单调递减,在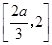 上单调递增,从而
上单调递增,从而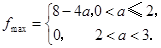
综上所述, 
考点:函数的最值
点评:该试题属于常规试题,解题的时候只要审题清晰,表示为数学代数式即可,让那后金额和函数求解最值。属于基础题。

练习册系列答案
相关题目
 .
. 时,求证:函数
时,求证:函数 在
在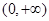 上单调递增;
上单调递增;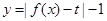 有三个零点,求
有三个零点,求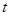 的值.
的值.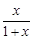 .
.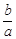 .
.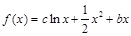
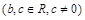 ,且
,且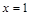 为
为 的极值点.
的极值点.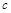 表示);
表示);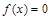 恰有两解,求实数
恰有两解,求实数
 ;
; ,求
,求 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;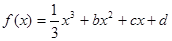 ,设曲线
,设曲线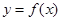 在与
在与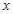 轴交点处的切线为
轴交点处的切线为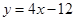 ,
,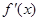 为
为 的导函数,满足
的导函数,满足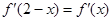 .
.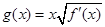 ,
,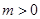 ,求函数
,求函数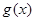 在
在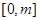 上的最大值;
上的最大值; ,
, ,
, 所围成的平面图形的面积。
所围成的平面图形的面积。 .
.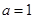 时,试判断
时,试判断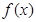 的单调性并给予证明;
的单调性并给予证明;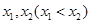 .
.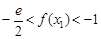 。 (注:
。 (注: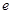 是自然对数的底数)
是自然对数的底数)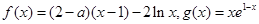 ,(
,(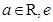 为自然对数的底数)。
为自然对数的底数)。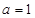 时,求函数
时,求函数 在区间
在区间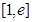 上的最大值和最小值;
上的最大值和最小值; 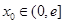 ,在
,在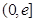 上总存在两个不同的
上总存在两个不同的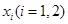 ,使得
,使得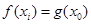 成立,求
成立,求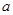 的取值范围。
的取值范围。