题目内容
(本题满分15分)
已知函数 .
.
(Ⅰ)当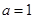 时,试判断
时,试判断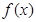 的单调性并给予证明;
的单调性并给予证明;
(Ⅱ)若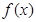 有两个极值点
有两个极值点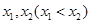 .
.
(i) 求实数a的取值范围;
(ii)证明: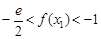 。 (注:
。 (注: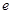 是自然对数的底数)
是自然对数的底数)
(1)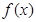 在R上单调递减 (2)
在R上单调递减 (2)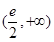 ,对于函数中不等式的证明,一般要功过构造函数来结合函数的最值来证明不等式的成立。
,对于函数中不等式的证明,一般要功过构造函数来结合函数的最值来证明不等式的成立。
解析试题分析:解:(1)当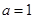 时,
时,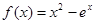 ,
,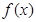 在R上单调递减 …………1分
在R上单调递减 …………1分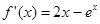 ,只要证明
,只要证明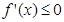 恒成立, …………………………2分
恒成立, …………………………2分
设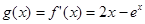 ,则
,则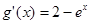 ,
,
当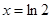 时,
时, ,
,
当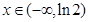 时,
时,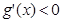 ,当
,当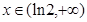 时,
时,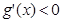 ………………4分
………………4分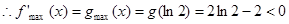 ,故
,故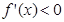 恒成立
恒成立
所以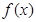 在R上单调递减 ……………………6分
在R上单调递减 ……………………6分
(2)(i)若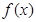 有两个极值点
有两个极值点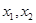 ,则
,则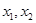 是方程
是方程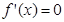 的两个根,
的两个根,
故方程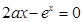 有两个根
有两个根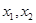 ,
,
又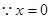 显然不是该方程的根,所以方程
显然不是该方程的根,所以方程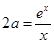 有两个根, …………8分
有两个根, …………8分
设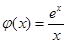 ,得
,得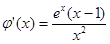
若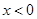 时,
时,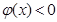 且
且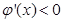 ,
,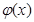 单调递减
单调递减
若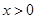 时,
时,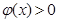
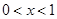 时
时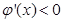 ,
,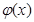 单调递减
单调递减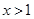 时
时 ,
,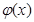 单调递增 ……………………………10分
单调递增 ……………………………10分
要使方程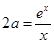 有两个根,需
有两个根,需 ,故
,故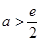 且
且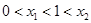
故 的取值范围为
的取值范围为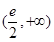 ……………………………………12分
……………………………………12分
法二:设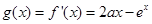 ,则
,则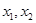 是方程
是方程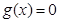 的两个根,
的两个根,
则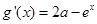 ,
,
当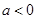 时,
时,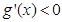 恒成立,
恒成立,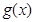 单调递减,方程
单调递减,方程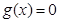 不可能有两个根
不可能有两个根
所以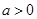 ,由
,由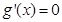 ,得
,得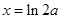 ,
,
当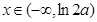 时,
时,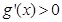 ,当
,当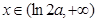 时,
时,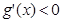
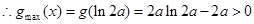 ,得
,得
(ii) 由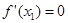 ,得:
,得: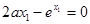 ,故
,故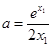 ,
,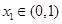
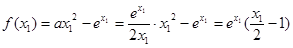 ,
,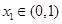 ………………14分
………………14分
设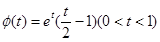 ,则
,则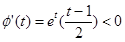 ,
,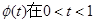 上单调递减
上单调递减

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
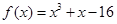 .
.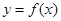 在点
在点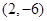 处的切线方程;
处的切线方程; 为曲线
为曲线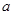 是实数,函数
是实数,函数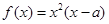 。
。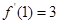 ,求
,求 在点
在点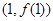 处的切线方程;
处的切线方程;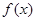 在区间
在区间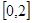 上的最大值。
上的最大值。 (a>0,b,cÎR),曲线
(a>0,b,cÎR),曲线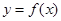 在点P(0,f (0))处的切线方程为
在点P(0,f (0))处的切线方程为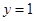 .
.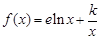 (其中e是自然对数的底数,k为正数)
(其中e是自然对数的底数,k为正数) 在
在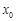 处取得极值,且
处取得极值,且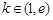 ,求
,求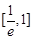 上的最大值.
上的最大值. .
.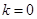 ,求
,求 的最小值;
的最小值;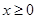 时
时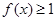 ,求实数
,求实数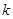 的取值范围.
的取值范围. 在
在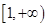 上为增函数,且
上为增函数,且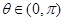 ,
,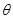 为常数,
为常数,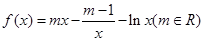 .
.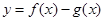 在
在 的取值范围;
的取值范围;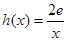 ,若在
,若在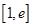 上至少存在一个
上至少存在一个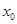 ,使得
,使得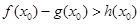 成立,求
成立,求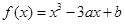 在
在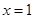 处有极小值
处有极小值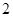 。
。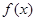 的解析式;
的解析式;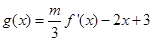 在
在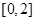 只有一个零点,求
只有一个零点,求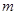 的取值范围。
的取值范围。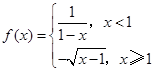 ,
,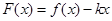 ,x∈R.试讨论函数F(x)的单调性.
,x∈R.试讨论函数F(x)的单调性.