题目内容
如图,在直三棱柱 中,
中, ,
, 分别是
分别是 的中点,且
的中点,且
 .
.
(1)求直线 与
与 所成角的大小;
所成角的大小;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)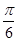 ;(2)
;(2)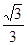 .
.
解析试题分析:由已知有AC、BC、CC1两两互相垂直,故可分别以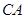 、
、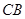 、
、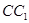 所在直线为
所在直线为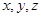 轴建立空间直角坐标系.然后由已知就可写出所需各点的空间坐标.(1)由此就可写出向量
轴建立空间直角坐标系.然后由已知就可写出所需各点的空间坐标.(1)由此就可写出向量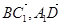 的坐标,然后再由两向量的夹角公式:
的坐标,然后再由两向量的夹角公式: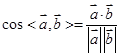 求出这两向量的夹角的余弦值,最后转化为对应两直线的夹角大小;只是应该注意两直线的夹角的取值范围是
求出这两向量的夹角的余弦值,最后转化为对应两直线的夹角大小;只是应该注意两直线的夹角的取值范围是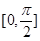 ,而两向量的夹角的取值范围是
,而两向量的夹角的取值范围是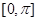 ;所以求出两向量的夹角的余弦值后取绝对值才是两直线的夹角的余弦值;(2)由中点坐标公式可求得点E的坐标,进而就可写出向量
;所以求出两向量的夹角的余弦值后取绝对值才是两直线的夹角的余弦值;(2)由中点坐标公式可求得点E的坐标,进而就可写出向量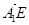 的坐标,再设平面
的坐标,再设平面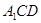 的一个法向量为
的一个法向量为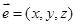 ,由
,由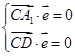 ,就可求出平面
,就可求出平面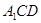 的一个法向量,从而就可求得这两向量夹角的余弦值,注意直线与平面所成的角的正弦值就等于直线的方向向量与平面法向量夹角的余弦值.
的一个法向量,从而就可求得这两向量夹角的余弦值,注意直线与平面所成的角的正弦值就等于直线的方向向量与平面法向量夹角的余弦值.
试题解析:解:分别以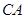 、
、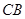 、
、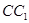 所在直线为
所在直线为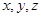 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则由题意可得: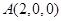 ,
,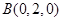 ,
,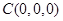 ,
,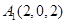 ,
,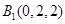 ,
,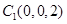 ,
,
又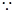
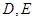 分别是
分别是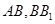 的中点,
的中点,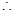
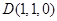 ,
,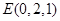 . 3分
. 3分
(1)因为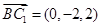 ,
, 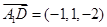 ,
,
所以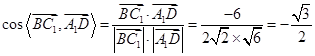 , 7分
, 7分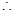 直线
直线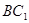 与
与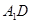 所成角的大小为
所成角的大小为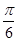 . 8分
. 8分
(2)设平面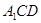 的一个法向量为
的一个法向量为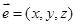 ,由
,由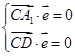 ,得
,得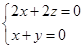 ,
,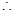 可取
可取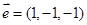 , 10分
, 10分
又
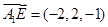 ,所以
,所以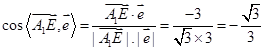 , 13分
, 13分 直线
直线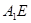 与平面
与平面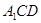 所成角的正弦值为
所成角的正弦值为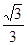 . 14分
. 14分
考点:1.异面直线所成的角;2.直线与平面所成的角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,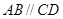 ,
,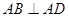 ,且
,且 .现以
.现以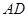 为一边向形外作正方形
为一边向形外作正方形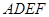 ,然后沿边
,然后沿边 为
为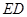 的中点,如图2.
的中点,如图2.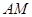 ∥平面
∥平面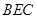 ;
;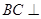 平面
平面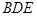 ;
; 到平面
到平面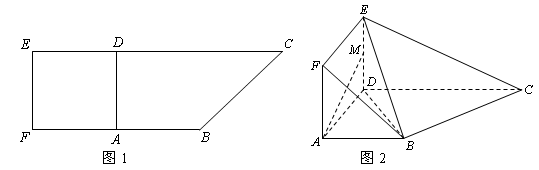
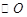 的直径AB=3,点C为
的直径AB=3,点C为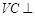 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点.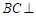 平面VAC;
平面VAC;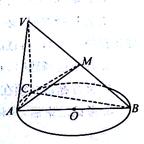
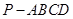 的底面为直角梯形,
的底面为直角梯形, ,
,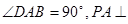 底面
底面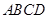 ,且
,且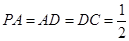 ,
,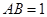 ,
,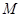 是
是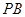 的中点.
的中点.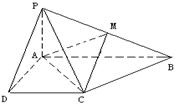
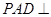 面
面 ;
;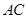 与
与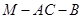 的正弦值.
的正弦值. 中,
中, 、
、 分别为
分别为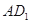 ,
, 中点。
中点。 与
与 所成角的大小;
所成角的大小; 平面
平面 。
。

 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中 ,
, 为侧棱
为侧棱 上的两个三等分点,如下图所示.
上的两个三等分点,如下图所示. ;
; 与
与 所成角的余弦值;
所成角的余弦值; 的余弦值.
的余弦值.