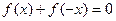题目内容
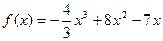
(Ⅰ)求
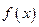 的单调区间和值域;
的单调区间和值域;(Ⅱ)设
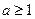 ,函数
,函数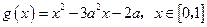 ,若对于任意
,若对于任意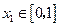 ,总存在
,总存在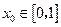 ,
,使得
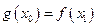 成立,求
成立,求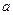 的取值范围
的取值范围(1)当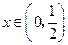 时,
时,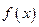 是减函数;当
是减函数;当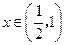 时,
时,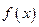 是增函数;
是增函数;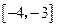
(2)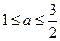
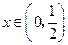 时,
时,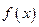 是减函数;当
是减函数;当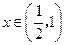 时,
时,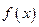 是增函数;
是增函数;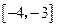
(2)
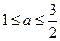
对函数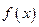 求导,得
求导,得
令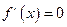 解得
解得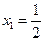 或
或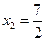
当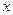 变化时,
变化时,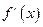 、
、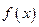 的变化情况如右表:
的变化情况如右表:
所以,当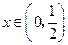 时,
时,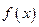 是减函数;当
是减函数;当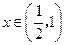 时,
时,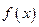 是增函数;
是增函数;
当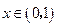 时,
时,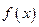 的值域为
的值域为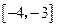
(Ⅱ)对函数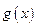 求导,得
求导,得 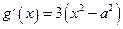
因此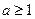 ,当
,当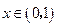 时,
时,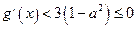
因此当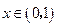 时,
时,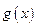 为减函数,从而当
为减函数,从而当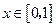 时有
时有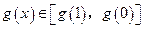
又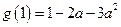 ,
,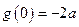 ,即当
,即当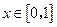 时有
时有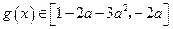
任给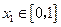 ,
,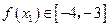 ,存在
,存在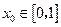 使得
使得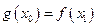 ,则
,则
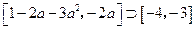 即
即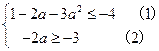 解
解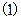 式得
式得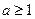 或
或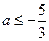
解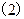 式得
式得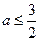 又
又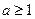 ,故:
,故: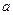 的取值范围为
的取值范围为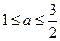
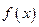 求导,得
求导,得
令
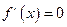 解得
解得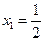 或
或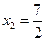
| x | 0 | 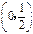 | 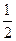 | 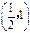 |  |
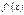 | | 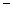 | 0 | 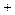 | |
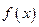 | 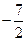 | 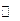 | 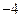 | 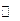 |  |
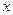 变化时,
变化时,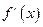 、
、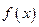 的变化情况如右表:
的变化情况如右表:所以,当
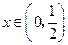 时,
时,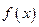 是减函数;当
是减函数;当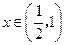 时,
时,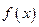 是增函数;
是增函数;当
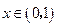 时,
时,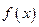 的值域为
的值域为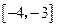
(Ⅱ)对函数
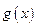 求导,得
求导,得 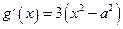
因此
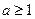 ,当
,当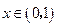 时,
时,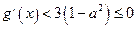
因此当
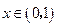 时,
时,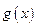 为减函数,从而当
为减函数,从而当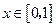 时有
时有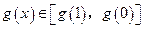
又
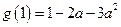 ,
,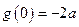 ,即当
,即当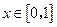 时有
时有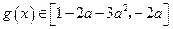
任给
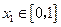 ,
,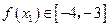 ,存在
,存在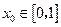 使得
使得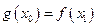 ,则
,则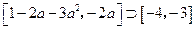 即
即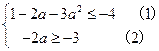 解
解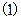 式得
式得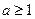 或
或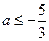
解
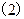 式得
式得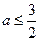 又
又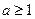 ,故:
,故: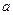 的取值范围为
的取值范围为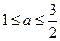

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
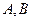 两地的距离是120km.假设汽油的价格是6元/升,以
两地的距离是120km.假设汽油的价格是6元/升,以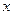 km/h(其中
km/h(其中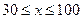 )速度行驶时,汽车的耗油率为
)速度行驶时,汽车的耗油率为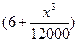 L/h,司机每小时的工资是28元.那么最经济的车速是多少?如不考虑其他费用,这次行车的总费用是多少?
L/h,司机每小时的工资是28元.那么最经济的车速是多少?如不考虑其他费用,这次行车的总费用是多少?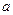
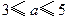
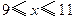
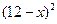
 (万元)与每件产品的售价
(万元)与每件产品的售价 出
出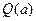
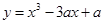 在
在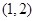 内有极小值,则实数
内有极小值,则实数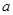 的取值范围是( )
的取值范围是( )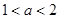
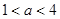
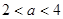

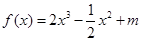 (
(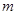 为常数)图象上
为常数)图象上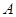 处的切线与直线
处的切线与直线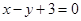 的夹角为45°,则点
的夹角为45°,则点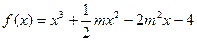 (m为常数,且m>0)有极大值
(m为常数,且m>0)有极大值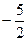 ,
,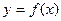 的斜率为2的切线方程.
的斜率为2的切线方程.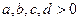 ,且不等于1,
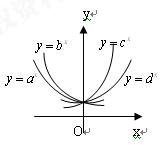
,且不等于1,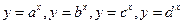 在同一坐标系中的图象如图,则
在同一坐标系中的图象如图,则 的大小顺序
的大小顺序  ( )
( )
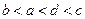
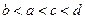
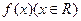 的一段图象如图所示,
的一段图象如图所示,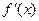 是函数
是函数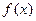 的导函数,且
的导函数,且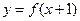 是奇函数,给出以下结论:
是奇函数,给出以下结论: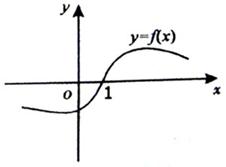
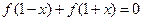 ;
;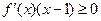 ;
;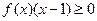 ;
;