题目内容
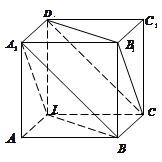
已知正方体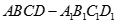 ,
, 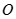 是底
是底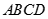 对角线的交点.
对角线的交点.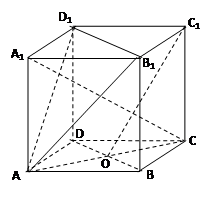
求证:(Ⅰ)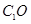 ∥面
∥面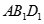 ;
;
(Ⅱ)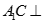 面
面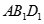
(Ⅰ)连结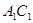 ,设
,设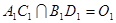 ,连结
,连结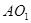 ,
,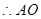

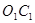 ,
, 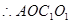 是平行四边形,
是平行四边形, 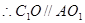 ,
,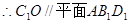 .
.
(Ⅱ)先证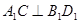 ,同理可证
,同理可证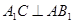 ,又
,又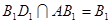 ,得到
,得到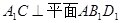 。
。
解析试题分析:(Ⅰ)连结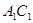 ,设
,设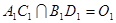 ,连结
,连结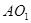 ,
,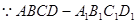 是正方体,
是正方体, 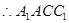 是平行四边形,
是平行四边形, 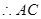

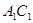 , 又
, 又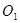 ,
,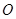 分别是
分别是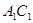 ,
,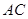 的中点,
的中点,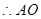

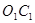 ,
, 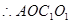 是平行四边形,
是平行四边形, 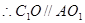 4分
4分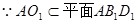 ,
,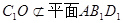
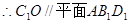 . 6分
. 6分
(Ⅱ) ,
,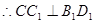 ,
,
又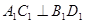 ,
, ,
, 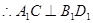 , 10分
, 10分
同理可证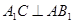 , 11分
, 11分
又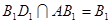 ,
,  , 13分
, 13分
考点:本题主要考查正方体的几何特征,立体几何中的平行关系、垂直关系。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。本题主要考查正方体的几何性质,难度不大。应注意规范写出证明过程。

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 中,求证:平面
中,求证:平面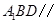 平面
平面 .
.
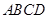 中,
中,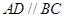 ,
,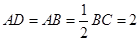 ,
,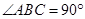 ,
,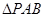 是等边三角形,平面
是等边三角形,平面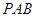 ⊥平面
⊥平面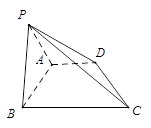
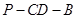 的余弦值;
的余弦值;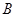 到平面
到平面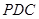 的距离.
的距离.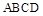 与
与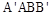 都是边长为
都是边长为 的正方形,点E是
的正方形,点E是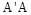 的中点,
的中点,
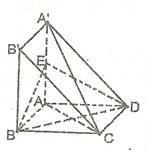
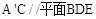 ;
;  ;
;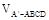 与
与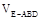 的比值。
的比值。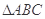 是等腰直角三角形,其中
是等腰直角三角形,其中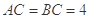 ,
,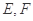 分别为
分别为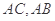 的中点,将
的中点,将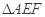 沿
沿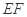 折起,点
折起,点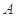 的位置变为点
的位置变为点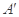 ,已知点
,已知点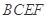 上的射影
上的射影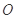 为
为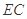 的中点,如图(2)所示.
的中点,如图(2)所示.
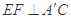 ;
;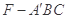 的体积.
的体积.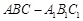 中,M、N分别是BC、AC1中点,AA1=2,AB=
中,M、N分别是BC、AC1中点,AA1=2,AB=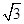 ,AC=AM=1.
,AC=AM=1.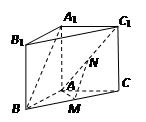
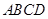 中,
中,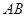 ,
, ,
, 两两互相垂直,且
两两互相垂直,且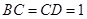 .
.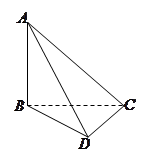
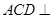 平面
平面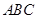 ;
;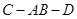 的大小;
的大小; 与平面
与平面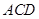 所成的角为
所成的角为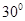 ,求线段
,求线段 的边长为
的边长为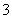 ,点
,点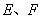 分别在
分别在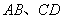 上,并且满足
上,并且满足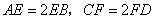 ,如图乙,将直角梯形
,如图乙,将直角梯形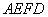 沿
沿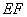 折到
折到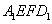 的位置,使点
的位置,使点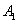 在
在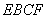 上的射影
上的射影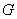 恰好在
恰好在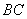 上.
上.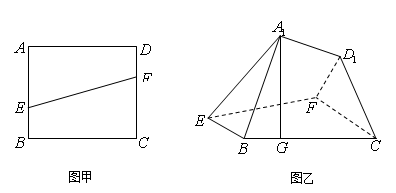
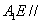 平面
平面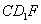 ;
;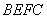 与平面
与平面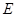 是以
是以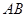 为直径的半圆上异于
为直径的半圆上异于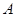 、
、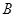 的点,矩形
的点,矩形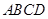 所在的平面垂直于该半圆所在的平面,且
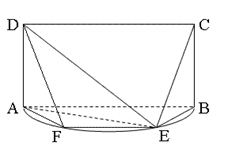
所在的平面垂直于该半圆所在的平面,且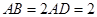 .
.
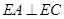 ;
;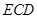 与半圆弧的另一个交点为
与半圆弧的另一个交点为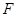 .
.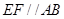 ;
;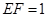 ,求三棱锥
,求三棱锥 的体积.
的体积.