题目内容
8.定义:对于数列{xn},如果存在常数p,使对任意正整数n,总有(xn+1-p)(xn-p)<0成立,那么我们称数列{xn}为“p-摆动数列”.(1)设an=2n-1,${b_n}={q^n}$(-1<q<0),n∈N*,判断数列{an}、{bn}是否为“p-摆动数列”,并说明理由;
(2)已知“p-摆动数列”{cn}满足:${c_{n+1}}=\frac{1}{{{c_n}+1}}$,c1=1.求常数p的值;
(3)设${d_n}={(-1)^n}•(\;2n-1)$,n∈N*,且数列{dn}的前n项和为Sn.求证:数列{Sn}是“p-摆动数列”,并求出常数p的取值范围.
分析 (1)假设数列{an}是“p-摆动数列”,即存在常数p,总有2n-1<p<2n+1对任意n成立,对n取值即可判断出.由${b_n}={q^n}$,于是${b_n}{b_{n+1}}={q^{2n+1}}<0$(-1<q<0)对任意n成立,即可判断出.
(2)由数列{cn}为“p-摆动数列”,c1=1$⇒{c_2}=\frac{1}{2}$,即存在常数$\frac{1}{2}<p<1$,使对任意正整数n,总有(cn+1-p)(cn-p)<0成立;即有(cn+2-p)(cn+1-p)<0成立.则(cn+2-p)(cn-p)>0,分别利用奇数项与偶数项的单调性即可得出.
(3)由${d_n}={(-1)^n}•(2n-1)$$⇒{S_n}={(-1)^n}•n$,显然存在p=0,使对任意正整数n,总有${S_n}{S_{n+1}}={(-1)^{2n+1}}•n(n+1)<0$成立,即可证明数列{Sn}是“p-摆动数列”;分别利用奇数项与偶数项的单调性即可得出p的取值范围.
解答 解:(1)假设数列{an}是“p-摆动数列”,
即存在常数p,总有2n-1<p<2n+1对任意n成立,
不妨取n=1时则1<p<3,取n=2时则3<p<5,显然常数p不存在,
∴数列{an}不是“p-摆动数列”;
由${b_n}={q^n}$,于是${b_n}{b_{n+1}}={q^{2n+1}}<0$对任意n成立,其中p=0.
∴数列{bn}是“p-摆动数列”.
(2)由数列{cn}为“p-摆动数列”,c1=1$⇒{c_2}=\frac{1}{2}$,
即存在常数$\frac{1}{2}<p<1$,使对任意正整数n,总有(cn+1-p)(cn-p)<0成立;
即有(cn+2-p)(cn+1-p)<0成立.
则(cn+2-p)(cn-p)>0,
∴c1>p>⇒c3>p⇒…⇒c2n-1>p.
同理c2<p⇒c4<p⇒…⇒c2n<p.
∴c2n<p<c2n-1⇒$\frac{1}{{{c_{2n-1}}+1}}<{c_{2n-1}}$,解得${c_{2n-1}}>\frac{{\sqrt{5}-1}}{2}$即$p≤\frac{{\sqrt{5}-1}}{2}$.
同理$\frac{1}{{{c_{2n}}+1}}>{c_{2n}}$,解得${c_{2n}}<\frac{{\sqrt{5}-1}}{2}$;即$p≥\frac{{\sqrt{5}-1}}{2}$.
综上$p=\frac{{\sqrt{5}-1}}{2}$.
(3)证明:由${d_n}={(-1)^n}•(2n-1)$$⇒{S_n}={(-1)^n}•n$,
显然存在p=0,使对任意正整数n,总有${S_n}{S_{n+1}}={(-1)^{2n+1}}•n(n+1)<0$成立,
∴数列{Sn}是“p-摆动数列”;
当n为奇数时Sn=-n递减,∴Sn≤S1=-1,只要p>-1即可,
当n为偶数时Sn=n递增,Sn≥S2=2,只要p<2即可,
综上-1<p<2,p的取值范围是(-1,2).
点评 本题考查了数列的单调性、新定义“p-摆动数列”、不等式的解法,考查了推理能力与计算能力,属于难题.

| A. | x=2是f(x)的极小值点 | |
| B. | 函数y=f(x)-x有且只有1个零点 | |
| C. | 存在正实数k,使得f(x)>kx恒成立 | |
| D. | 对任意两个正实数x1,x2,且x2>x1,若f(x1)=f(x2),则x1+x2>4 |
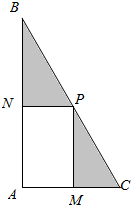 某中学为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].
某中学为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].