题目内容
(本小题满分10分)求直线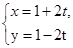
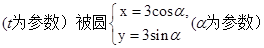 截得的弦长.
截得的弦长.
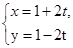
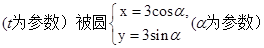 截得的弦长.
截得的弦长.解:将直线方程化为普通方程为:x+y=2,
将圆C的方程化为普通方程为:x2+y2=9,
则圆心到直线l的距离d=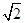 ,
,
∴所求弦长为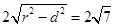
将圆C的方程化为普通方程为:x2+y2=9,
则圆心到直线l的距离d=
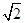 ,
,∴所求弦长为
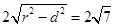
本试题主要是考查了直线与圆的位置关系的运用求解相交的弦长问题。先求解圆心,以及圆心到直线的距离,利用勾股定理得到结论。
解:将直线方程化为普通方程为:x+y=2,
将圆C的方程化为普通方程为:x2+y2=9,
则圆心到直线l的距离d=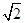 ,
,
∴所求弦长为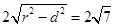
解:将直线方程化为普通方程为:x+y=2,
将圆C的方程化为普通方程为:x2+y2=9,
则圆心到直线l的距离d=
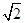 ,
,∴所求弦长为
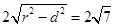

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
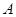 的极坐标为
的极坐标为 ,直线
,直线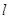 过点
过点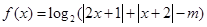 ,若关于
,若关于 的不等式
的不等式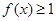 的解集为
的解集为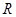 ,则
,则 的取值范围是 .
的取值范围是 . 外的一点
外的一点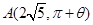 (其中
(其中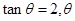 为锐角)作平行于
为锐角)作平行于 的直线
的直线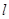 与曲线分别交于
与曲线分别交于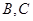 .
.  和直线
和直线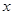 轴的正半轴建系);
轴的正半轴建系); 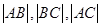 成等比数列,求
成等比数列,求 的值.
的值.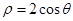 的圆心到直线
的圆心到直线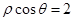 的距离是_____________.
的距离是_____________. 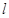 的方程为
的方程为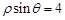 ,则点
,则点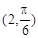 到直线
到直线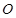 为极点,
为极点,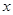 轴的非负半轴为极轴建立极坐标系。已知点
轴的非负半轴为极轴建立极坐标系。已知点 的极坐标为
的极坐标为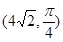 ,曲线
,曲线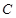 的参数方程为
的参数方程为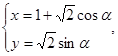 (
(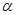 为参数)。
为参数)。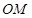 的直角坐标方程;
的直角坐标方程;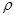 cos (θ-
cos (θ-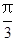 )=1,曲线C2的方程为
)=1,曲线C2的方程为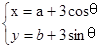 .(θ为参数,θ
.(θ为参数,θ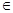 [o,2π)),a,b为实常数,当点(a,b)与曲线C1上点间的最小距离为
[o,2π)),a,b为实常数,当点(a,b)与曲线C1上点间的最小距离为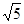 时,则C1与C2交点间的距离为
时,则C1与C2交点间的距离为 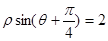 被圆
被圆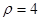 截得的弦长为 。
截得的弦长为 。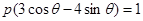 ,则C与极轴的交点到极点的距离是 .
,则C与极轴的交点到极点的距离是 .