题目内容
在直角坐标平面内,以坐标原点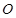 为极点,
为极点,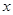 轴的非负半轴为极轴建立极坐标系。已知点
轴的非负半轴为极轴建立极坐标系。已知点 的极坐标为
的极坐标为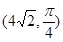 ,曲线
,曲线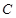 的参数方程为
的参数方程为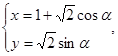 (
(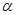 为参数)。
为参数)。
(Ⅰ)求直线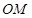 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求点 到曲线
到曲线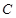 上的点的距离的最小值。
上的点的距离的最小值。
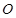 为极点,
为极点,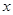 轴的非负半轴为极轴建立极坐标系。已知点
轴的非负半轴为极轴建立极坐标系。已知点 的极坐标为
的极坐标为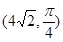 ,曲线
,曲线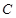 的参数方程为
的参数方程为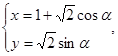 (
(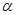 为参数)。
为参数)。(Ⅰ)求直线
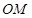 的直角坐标方程;
的直角坐标方程;(Ⅱ)求点
 到曲线
到曲线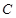 上的点的距离的最小值。
上的点的距离的最小值。解:(Ⅰ)由点M的极坐标为 得点M的直角坐标为
得点M的直角坐标为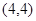 , 2分
, 2分
所以直线OM的直角坐标方程为 。 3分
。 3分
(Ⅱ)由曲线C的参数方程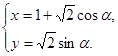 (
(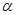 为参数)。
为参数)。
化为普通方程为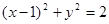 , 5分
, 5分
圆心为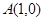 ,半径为
,半径为 。 6分
。 6分
由于点M在曲线C外,故点M到曲线C上的点的距离最小值为 。
。
8分
 得点M的直角坐标为
得点M的直角坐标为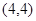 , 2分
, 2分所以直线OM的直角坐标方程为
 。 3分
。 3分(Ⅱ)由曲线C的参数方程
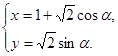 (
(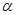 为参数)。
为参数)。化为普通方程为
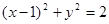 , 5分
, 5分圆心为
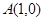 ,半径为
,半径为 。 6分
。 6分由于点M在曲线C外,故点M到曲线C上的点的距离最小值为
 。
。 8分
本试题主要是考查了极坐标系下的返程和点到曲线的距离的最值。
(1)由极坐标方程可知点由点M的直角坐标的(4,4),从而得到直线OM的直角坐标方程
(2)由于曲线为圆,那么点到圆上点距离的的最小值可以用圆心到点的距离减去圆的半径即可。
(1)由极坐标方程可知点由点M的直角坐标的(4,4),从而得到直线OM的直角坐标方程
(2)由于曲线为圆,那么点到圆上点距离的的最小值可以用圆心到点的距离减去圆的半径即可。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目




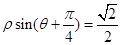 ,则极点到这条直线的距离是 .
,则极点到这条直线的距离是 . 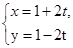
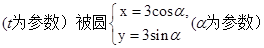 截得的弦长.
截得的弦长.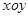 内,直线
内,直线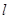 的参数方程
的参数方程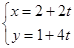 (
(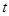 为参数),以
为参数),以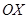 为极轴建立极坐标系,圆
为极轴建立极坐标系,圆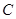 的极坐标方程为
的极坐标方程为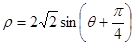 .
.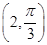 到圆ρ=2cosθ的圆心的距离为
到圆ρ=2cosθ的圆心的距离为
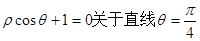 对称的曲线的极坐标方程是_____________。
对称的曲线的极坐标方程是_____________。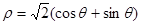 的圆心坐标是( )
的圆心坐标是( )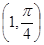
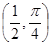
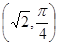
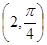
 到直线
到直线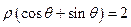 的距离为
的距离为