题目内容
【题目】四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() .
.![]() ,且
,且![]() 平面
平面![]() ,
,![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的中点,
上的中点,![]() 在
在![]() 上.且
上.且![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 的成角的正弦值;
的成角的正弦值;
(Ⅲ)请画出平面![]() 与四棱锥的表面的交线,并写出作图的步骤.
与四棱锥的表面的交线,并写出作图的步骤.
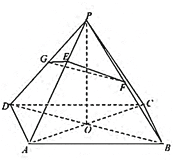
【答案】(1)见解析(2)![]() (3)四边形
(3)四边形![]() 为平面
为平面![]() 与四棱锥的表面的交线
与四棱锥的表面的交线
【解析】分析:(Ⅰ)推导出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;
;
(Ⅱ)推导出![]() ,
,![]() ,
,![]() ,以O为原点,OA、OB、OP分别为x、y、z轴建立空间直角做消息,利用向量法能求出直线AB与平面EFG的所成角的正弦值;
,以O为原点,OA、OB、OP分别为x、y、z轴建立空间直角做消息,利用向量法能求出直线AB与平面EFG的所成角的正弦值;
(Ⅲ)法1:延长![]() 分别交
分别交![]() 延长线于
延长线于![]() ,连接
,连接![]() ,发现刚好过点
,发现刚好过点![]() ,,连接
,,连接![]() ,则四边形
,则四边形![]() 为平面
为平面![]() 与四棱锥的表面的交线.
与四棱锥的表面的交线.
法2:记平面![]() 与直线
与直线![]() 的交点为
的交点为![]() ,设
,设![]() ,,利用向量法求出
,,利用向量法求出![]() ,从而
,从而![]() 即为点
即为点![]() .连接
.连接![]() ,
,![]() ,则四边形
,则四边形![]() 为平面
为平面![]() 与四棱锥的表面的交线.
与四棱锥的表面的交线.
解析:解:(Ⅰ)在![]() 中,因为点
中,因为点![]() 分别是线段
分别是线段![]() 上的中点,
上的中点,
所以![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
(Ⅱ)因为底面![]() 是边长为2的菱形,
是边长为2的菱形,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
如图,建立空间直角坐标系,则依题意可得
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
, ![]()
设平面![]() 的法向量为
的法向量为![]() ,则由
,则由![]() 可得
可得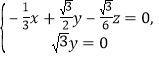 ,
,
令![]() ,可得
,可得![]()
因为![]() .
.
所以直线![]() 与平面
与平面![]() 的成角的正弦值为
的成角的正弦值为![]()
(Ⅲ)法Ⅰ:延长![]() 分别交
分别交![]() 延长线于
延长线于![]() ,连接
,连接![]() ,发现刚好过点
,发现刚好过点![]() ,,连接
,,连接![]() ,则四边形
,则四边形![]() 为平面
为平面![]() 与四棱锥的表面的交线.
与四棱锥的表面的交线.
法2:记平面![]() 与直线
与直线![]() 的交点为
的交点为![]() ,设
,设![]() ,则
,则![]()
由![]() ,可得
,可得![]() .
.
所以![]() 即为点
即为点![]() .
.
所以连接![]() ,
,![]() ,则四边形
,则四边形![]() 为平面
为平面![]() 与四棱锥的表面的交线.
与四棱锥的表面的交线.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325 8430 8215 7453 7446 6754
7638 6834 6460 6830 9860 8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为![]() )
)
组别 | 步数分组 | 频数 |
|
| 2 |
|
| 10 |
|
|
|
|
| 2 |
|
|
|
(Ⅰ)写出![]() 的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
(Ⅱ)记![]() 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为![]() ,
,![]() ,
,![]() 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为![]() ,
,![]() ,试分别比较
,试分别比较![]() 与以
与以![]() ,
,![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从上述![]() 两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为
两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.