��Ŀ����
����Ŀ���Ӽ�����ijУ��һ��1000��ѧ�������ȡ50���������п�����ѧ�ɼ�������ȡѧ���ɼ�ȫ������95�ֺ�135��֮�䣬����ȡ�ijɼ��ֳɰ��飺��һ��[95��100]���ڶ���[100��105]�������ڰ���[130��135]����ͼ�ǰ���������õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪ǰ����������ɵȲ����У������������Ϊ4�ˣ���һ��������ǵ����顢�ڰ�������֮�ͣ� 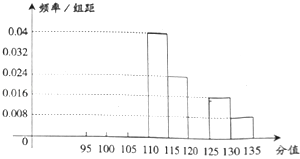
��1����ͼ�ϲ�ȫƵ�ʷֲ�ֱ��ͼ�������Ƹ�У1000��ѧ���гɼ���120�����ϣ���120�֣���������
��2�����ӳɼ����ڵ����飬�ڰ��������ѧ���������ȡ����ѧ���������ǵijɼ��ֱ�Ϊx��y���¼�G=||x��y|��5|����P��G����
���𰸡�
��1���⣺������ã���������10������������6������������4�����ڰ�����2����
��ǰ���鹲��24����
ǰ����������ɵȲ����У���һ����6����
��ڶ���8����������10����
�ɴ�����Ƶ�ʷֲ�ֱ��ͼ������ͼ��
��Ƶ�ʷֲ�ֱ��ͼ�óɼ���120�����ϣ���120�֣���Ƶ��Ϊ����0.016+0.016+0.008����5=0.2��
���Ƹ�У1000��ѧ���гɼ���120�����ϣ���120�֣�������Ϊ��1000��0.2=200��
��2���⣺�ǵ�����4��ѧ��Ϊa��b��c��d��
�ڰ���2��ѧ��ΪE��F��
����ѧ���������ȡ����ѧ����ab��ac��ad��aE��aF��bc��bd��bE��bF��cd��cE��cF��dE��dF��EF����15�������
���¼�G����ab��ac��ad��bc��bd��cd��EF��7�������
���¼�G=||x��y|��5|�ĸ���P��G��= ![]() ��
��

����������1��������ã���������10������������6������������4�����ڰ�����2�����Ӷ�ǰ���鹲��24����������һ����6�����ڶ���8����������10�����ɴ�����Ƶ�ʷֲ�ֱ��ͼ�����Ƹ�У1000��ѧ���гɼ���120�����ϣ���120�֣�����������2���ǵ�����4��ѧ��Ϊa��b��c��d���ڰ���2��ѧ��ΪE��F���ɴ������оٷ�������¼�G=||x��y|��5|�ĸ���P��G����
�����㾫����ͨ���������Ƶ�ʷֲ�ֱ��ͼ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ�����Խ����⣮