题目内容
给出下列命题:
①y=1是幂函数;
②函数f(x)=2x-x2的零点有2个;
③(x+
+2)5展开式的项数是6项;
④函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积是S=
sinxdx;
⑤若ξ~N(1,σ2),且P(0≤ξ≤1)=0.3,则P(ξ≥2)=0.2;
其中真命题的序号是 (写出所有正确命题的编号).
①y=1是幂函数;
②函数f(x)=2x-x2的零点有2个;
③(x+
| 1 |
| x |
④函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积是S=
| ∫ | π -π |
⑤若ξ~N(1,σ2),且P(0≤ξ≤1)=0.3,则P(ξ≥2)=0.2;
其中真命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用,概率与统计,二项式定理
分析:①,利用幂函数的概念可判断①错误;
②,作出函数f(x)=2x-x2的图象,可判断②错误;
③,将原式化为(x+
+2)5=
,利用二项式定理可知,展开式的项数,可判断③错误;
④,利用微积分定理可求得函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积,再计算S=
sinxdx,可判断④错误;
⑤,利用正态密度分别曲线的性质,可知P(1≤ξ≤2)=0.3,P(ξ≥2)=
=
=0.2,可判断⑤正确.
②,作出函数f(x)=2x-x2的图象,可判断②错误;
③,将原式化为(x+
| 1 |
| x |
| (x+1)10 |
| x5 |
④,利用微积分定理可求得函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积,再计算S=
| ∫ | π -π |
⑤,利用正态密度分别曲线的性质,可知P(1≤ξ≤2)=0.3,P(ξ≥2)=
| 1-2P(0≤ξ≤1) |
| 2 |
| 1-0.3×2 |
| 2 |
解答:
解:对于①,y=x0(x≠0)是幂函数,但y=1不是幂函数,故①错误;
对于②,由图可知,函数f(x)=2x-x2的零点有3个,故②错误;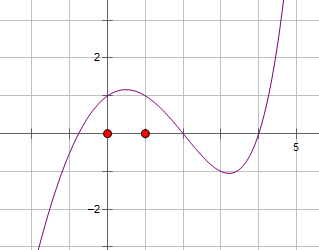
对于③,(x+
+2)5=[
]5=
展开式的项数是11项,故③错误;
对于④,函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积是S=2
sinxdx=-2cosx
=2,
又
sinxdx=-cosx
=-[cosπ-cos(-π)]=0,显然2≠0,故④错误;
对于⑤,因为ξ~N(1,σ2),且P(0≤ξ≤1)=0.3,故P(1≤ξ≤2)=0.3,
所以则P(ξ≥2)=
=
=0.2,故⑤正确;
故答案为:⑤.
对于②,由图可知,函数f(x)=2x-x2的零点有3个,故②错误;

对于③,(x+
| 1 |
| x |
| (x+1)2 |
| x |
| (x+1)10 |
| x5 |
对于④,函数y=sinx(x∈[-π,π])图象与x轴围成的图形的面积是S=2
| ∫ | π 0 |
| | | π 0 |
又
| ∫ | π -π |
| | | π -π |
对于⑤,因为ξ~N(1,σ2),且P(0≤ξ≤1)=0.3,故P(1≤ξ≤2)=0.3,
所以则P(ξ≥2)=
| 1-2P(0≤ξ≤1) |
| 2 |
| 1-0.3×2 |
| 2 |
故答案为:⑤.
点评:本题考查命题的真假判断与应用,综合考查幂函数的概念、函数的零点、二项式定理的应用及定积分、正态密度曲线的性质及应用,考查转化思想与作图、分析、运算等综合能力,是难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
“sinθ=
”是“θ=
”的( )
| ||
| 2 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在△ABC中,下列等式恒成立的是( )
| A、csinA=asinB |
| B、bcosA=acosB |
| C、asinA=bsinB |
| D、asinB=bsinA |
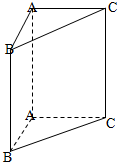 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=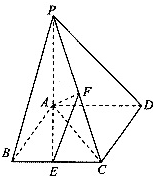 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.