题目内容
2.由棱长为2的正方体表面的六个中心为顶点构成的新几何体的体积为( )| A. | 2 | B. | 4 | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
分析 由棱长为2的正方体表面的六个中心为顶点构成的新几何体是两个有公共底的正四棱锥,正四棱锥的底面是边长为$\sqrt{2}$,高为1,由此能求出新几何体的体积.
解答 解:如图,由棱长为2的正方体表面的六个中心为顶点构成的新几何体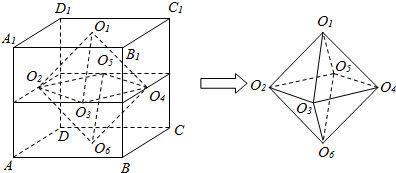
是两个有公共底的正四棱锥O1-O2O3O4O5-O6,
正四棱锥的底面O2O3O4O5是边长为$\sqrt{2}$的正方形,正四棱锥高为1,
∴正四棱锥O1-O2O3O4O5的体积V′=$\frac{1}{3}×{(\sqrt{2})}^{2}×1$=$\frac{2}{3}$,
∴新几何体的体积为V=2V′=$\frac{4}{3}$.
故选:D.
点评 本题考查几何体的体积的求法,是基础题,解题时要认真审题,解题的关键是得到新几何体是两个有公共底的正四棱锥,且正四棱锥的底面是边长为$\sqrt{2}$的正方形,高为1.

练习册系列答案
相关题目
13.若关于x的方程x3-3x+a=0有三个不同的实数解,则实数a的取值范围( )
| A. | -2<a≤0 | B. | 0≤a<2 | C. | -2<a<2 | D. | -2≤a≤2 |
7.函数f(x)是奇函数,当x≥0时f(x)=x(x+1),则当x<0时f(x)=( )
| A. | x(-x+1) | B. | -x(-x+1) | C. | x(x+1) | D. | -x(x+1) |
11.若0<a<1,-1<b<0,则函数y=ax+b的图象必不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
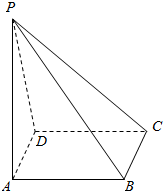 如图,四棱锥P-ABCD底面是边长为2的正方形,侧面PAD是等边三角形,且侧面PAD⊥底面ABCD,则侧棱PC与底面ABCD夹角的正弦值为$\frac{{\sqrt{6}}}{4}$.
如图,四棱锥P-ABCD底面是边长为2的正方形,侧面PAD是等边三角形,且侧面PAD⊥底面ABCD,则侧棱PC与底面ABCD夹角的正弦值为$\frac{{\sqrt{6}}}{4}$.