题目内容
【题目】通过随机询问
名不同性别的大学生在购买食物时是否看营养说明，得到如下列联表：
男 | 女 | 总计 | |
读营养说明 |
|
|
|
不读营养说明 |
|
|
|
总计 |
|
|
|
附：
|
|
|
|
|
|
|
|
（1）由以上列联表判断，能否在犯错误的概率不超过
的前提下认为性别和是否看营养说明有关系呢？
（2）从被询问的
名不读营养说明的大学生中随机选取
名学生，求抽到女生人数
的分布列及数学期望.
【答案】(1) 在犯错误的概率不超过
的前提下认为“性别与读营养说明之间有关系”.
（2）分布列见解析；
.
【解析】分析：(1)先根据卡方公式计算
，再与参考数据比较作判断，（2）先确定随机变量得取法，再利用组合数求对应概率，列表得分布列，最后根据数学期望公式求期望.
详解： （1）由计算可得的观测值为
因为
，而
所以在犯错误的概率不超过的前提下认为“性别与读营养说明之间有关系”
（2）
的取值为
，
，
，
的分布列为
|
|
|
|
|
|
|
|
的数学期望
【题目】在地面上同一地点观测远方匀速垂直上升的热气球，在上午10点整热气球的仰角是
，到上午10点20分的仰角变成
.请利用下表判断到上午11点整时，热气球的仰角最接近哪个度数( )
|
|
|
|
|
|
|
|
|
|
| 0.5 | 0.559 | 0.629 | 0.643 | 0.656 | 0.669 | 0.682 | 0.695 | 0.707 |
| 0.866 | 0.829 | 0.777 | 0.766 | 0.755 | 0.743 | 0.731 | 0.719 | 0.707 |
| 0.577 | 0.675 | 0.810 | 0.839 | 0.869 | 0.900 | 0.933 | 0.966 | 1.0 |
A. 
B. 
C. 
D. 
【题目】全世界越来越关注环境保护问题，某监测站点于2018年1月某日起连续
天监测空气质量指数(
)，数据统计如下：
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
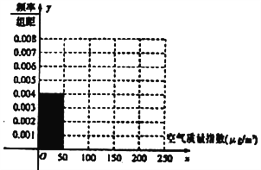
（1）根据所给统计表和频率分布直方图中的信息求出，
的值，并完成频率分布直方图；
（2）由频率分布直方图，求该组数据的众数和中位数；
（3）在空气质量指数分别属于
和
的监测数据中，用分层抽样的方法抽取
天，再从中任意选取
天，求事件
“两天空气都为良”发生的概率.
