题目内容
2.在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1,直线B1C与平面ABC成30°角.(I)求证:平面B1AC⊥平面ABB1A1;
(Ⅱ)求直线A1C与平面B1AC所成角的正弦值;
(Ⅲ)求二面角B-B1C-A的大小.
分析 (Ⅰ)根据已知条件知A1C1,A1B1,A1A三直线两两垂直,从而可分别以这三直线为x,y,z轴,建立空间直角坐标系,求出图形上各点的坐标.设平面B1AC的法向量为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,根据$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=0}\\{\overrightarrow{m}•\overrightarrow{{B}_{1}C}=0}\end{array}\right.$即可求出$\overrightarrow{m}$,而由条件知$\overrightarrow{{A}_{1}{C}_{1}}$为平面ABB1A1的一条法向量,只要$\overrightarrow{m}•\overrightarrow{{A}_{1}{C}_{1}}=0$即可得出平面B1AC⊥平面ABB1A1;
(Ⅱ)求出$\overrightarrow{{A}_{1}C}=(\sqrt{2},0,1)$,设直线A1C和平面B1AC所成角为θ,则由sinθ=|cos$<\overrightarrow{{A}_{1}C},\overrightarrow{m}>$|=$\frac{|\overrightarrow{{A}_{1}C}•\overrightarrow{m}|}{|\overrightarrow{{A}_{1}C}||\overrightarrow{m}|}$即可求得sinθ;
(Ⅲ)设平面BB1C的法向量为$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$,设二面角B-B1C-A的大小为α,由cos$α=cos<\overrightarrow{m},\overrightarrow{n}>$即可求得cosα,从而求出二面角B-B1C-A的大小.
解答 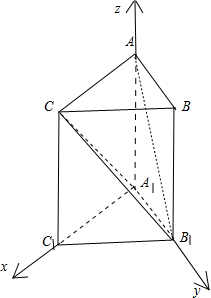 解:(Ⅰ)证明:根据条件知A1C1,A1B1,A1A三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系;
解:(Ⅰ)证明:根据条件知A1C1,A1B1,A1A三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系;
设AB=BB1=1,BB1⊥平面ABC,∴∠B1CB为直线B1C与平面ABC所成角;
∴∠B1CB=30°;
∴$BC=\sqrt{3}$,∠BAC=90°,∴$AC=\sqrt{2}$,所以:
A1(0,0,0),A(0,0,1),B(0,1,1),C($\sqrt{2}$,0,1),${B}_{1}(0,1,0),{C}_{1}(\sqrt{2},0,0)$;
设平面B1AC的法向量为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,$\overrightarrow{AC}=(\sqrt{2},0,0),\overrightarrow{{B}_{1}C}=(\sqrt{2},-1,1)$,则:
$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=\sqrt{2}{x}_{1}=0}\\{\overrightarrow{m}•\overrightarrow{{B}_{1}C}=\sqrt{2}{x}_{1}-{y}_{1}+{z}_{1}=0}\end{array}\right.$,取z1=1,∴$\overrightarrow{m}=(0,1,1)$;
A1C1⊥A1B1,A1C1⊥AA1,AA1∩A1B1=A1;
∴A1C1⊥平面ABB1A1;
∴$\overrightarrow{{A}_{1}{C}_{1}}=(\sqrt{2},0,0)$为平面ABB1A1的一条法向量;
∴$\overrightarrow{m}•\overrightarrow{{A}_{1}{C}_{1}}=0$;
∴平面B1AC⊥平面ABB1A1;
(Ⅱ)$\overrightarrow{{A}_{1}C}=(\sqrt{2},0,1)$,设直线A1C与平面B1AC所成角为θ,则:
sinθ=$|cos<\overrightarrow{{A}_{1}C},\overrightarrow{m}>|=\frac{1}{\sqrt{2}•\sqrt{3}}=\frac{\sqrt{6}}{6}$;
∴直线A1C与平面B1AC所成角为$\frac{\sqrt{6}}{6}$;
(Ⅲ)设平面BB1C的法向量为$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$,$\overrightarrow{{B}_{1}C}=(\sqrt{2},-1,1),\overrightarrow{{B}_{1}B}=(0,0,1)$,则:
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{B}_{1}C}=\sqrt{2}{x}_{2}-{y}_{2}+{z}_{2}=0}\\{\overrightarrow{n}•\overrightarrow{{B}_{1}B}={z}_{2}=0}\end{array}\right.$,取x2=1,则$\overrightarrow{n}=(1,\sqrt{2},0)$;
又平面B1AC的一条法向量为$\overrightarrow{m}=(0,1,1)$,设二面角B-B1C-A的大小为α,则:
$cosα=cos<\overrightarrow{m},\overrightarrow{n}>=\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{\sqrt{2}}{\sqrt{2}•\sqrt{3}}$=$\frac{\sqrt{3}}{3}$;
∴二面角B-B1C-A的大小为arc$cos\frac{\sqrt{3}}{3}$.
点评 考查平面法向量的概念及求法,向量垂直的充要条件,知道两平面垂直时,两平面法向量的关系,弄清直线和平面所成角与直线的方向向量和平面法向量夹角的关系,向量夹角余弦的坐标公式,弄清两平面形成二面角和平面法向量间夹角的关系.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
| A. | $\frac{8}{3}$ | B. | 8 | C. | 4 | D. | $\frac{4}{3}$ |
| A. | 3 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |