题目内容
【题目】已知函数![]() ,
,
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 有两个零点
有两个零点![]() ,(
,(![]() ),求证:
),求证: ![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)去绝对值,分为![]() 时,
时, ![]() ,函数单调递增;当
,函数单调递增;当![]() 时,根据导数与0的关系得其单调性;(2)由(1)知,当
时,根据导数与0的关系得其单调性;(2)由(1)知,当![]() 时,函数
时,函数![]() 单调递增,函数至多只有一个零点,不合题意;则必有
单调递增,函数至多只有一个零点,不合题意;则必有![]() ,此时函数
,此时函数![]() 的单调递减区间为
的单调递减区间为![]() ;单调递增区间为
;单调递增区间为![]() ,进一步得出
,进一步得出![]() 和
和![]() ,从而得出答案.
,从而得出答案.
试题解析:(1)依题意有,函数的定义域为![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() ,函数
,函数![]() 的单调增区间为
的单调增区间为![]() , 当
, 当![]() 时,
时, 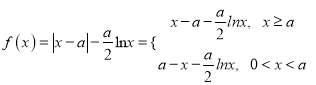 ,若
,若![]() ,
, ![]() ,此时函数单调递增, 若
,此时函数单调递增, 若![]() ,
, ![]() ,此时函数单调递减,综上所述,当
,此时函数单调递减,综上所述,当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,当
,当![]() 时,函数
时,函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]()
(2)由(1)知,当![]() 时,函数
时,函数![]() 单调递增,至多只有一个零点,不合题意;则必有
单调递增,至多只有一个零点,不合题意;则必有![]() , 此时函数
, 此时函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,由题意,必须
,由题意,必须![]() ,解得
,解得![]() 由
由![]() ,
, ![]() ,得
,得![]() ,而
,而![]() ,下面证明:
,下面证明: ![]() 时,
时, ![]()
设![]() ,(
,(![]() ),则
),则![]() ,所以
,所以![]() 在
在![]() 时递增,则
时递增,则![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,综上所述,
,综上所述, ![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095﹣2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如表所示:
PM2.5日均值 | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
频数 | 3 | 1 | 1 | 1 | 1 | 3 |
(1)从这10天的PM2.5日均值监测数据中,随机抽取3天,求恰有1天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列;
(3)以这10天的PM2.5日均值来估计一年的空气质量状况,则一年(按366天算)中平均有多少天的空气质量达到一级或二级.(精确到整数)