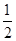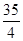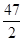题目内容
 是定义在
是定义在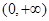 上的非负可导函数,且满足
上的非负可导函数,且满足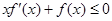 ,对任意正数
,对任意正数 ,若
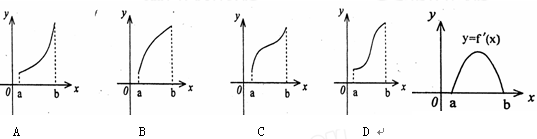
,若 ,则必有( )
,则必有( )
A.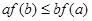 | B.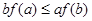 | C.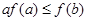 | D.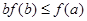 |
A
解析试题分析:由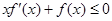 可得
可得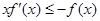 ,因为
,因为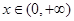 且
且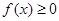 ,所以
,所以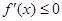 在
在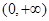 上恒成立,所以
上恒成立,所以 在
在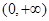 单调递减或
单调递减或 为非负的常数函数(当且仅当
为非负的常数函数(当且仅当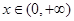 时,都有
时,都有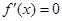 时,
时, 才为常数函数),当
才为常数函数),当 在
在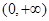 单调递减时,由
单调递减时,由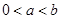 可得
可得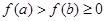 ,再由不等式性质中的可乘性可得
,再由不等式性质中的可乘性可得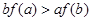 ;当
;当 为非负常数函数时,
为非负常数函数时,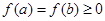 ,所以
,所以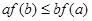 (当且仅当
(当且仅当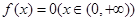 时,等号成立),综上可知,选A.
时,等号成立),综上可知,选A.
本题条件“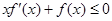 ”所得结论的另一种情况,因为
”所得结论的另一种情况,因为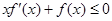 即
即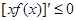 ,设
,设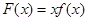 ,则
,则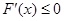 ,所以
,所以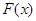 在
在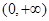 单调递减或
单调递减或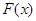 为恒大于零的常数函数(当且仅当
为恒大于零的常数函数(当且仅当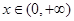 时,都有
时,都有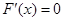 时,
时,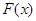 才为常数函数),当
才为常数函数),当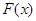 在
在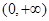 单调递减时,由
单调递减时,由 ,可得
,可得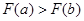 即
即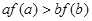 ;当
;当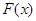 为恒大于零的常数函数时,
为恒大于零的常数函数时,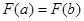 即
即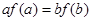 ,综上可知,
,综上可知,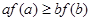 ,但本题并无此答案,所以只能是A答案.
,但本题并无此答案,所以只能是A答案.
考点:函数的单调性与导数.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
已知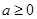 ,函数
,函数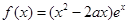 ,若
,若 在
在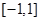 上是单调减函数,则
上是单调减函数,则 的取值范围是( )
的取值范围是( )
A.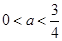 | B.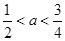 | C.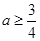 | D.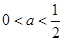 |
定积分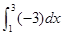 等于( )
等于( )
A.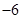 | B.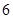 | C. | D. |
设函数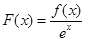 是定义在
是定义在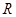 上的函数,其中
上的函数,其中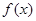 的导函数为
的导函数为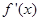 ,满足
,满足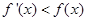 对于
对于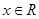 恒成立,则
恒成立,则
A.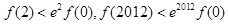 | B.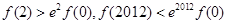 |
C.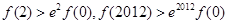 | D.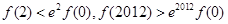 |
已知函数f(x)=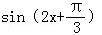 ,要得到
,要得到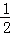 f′(x)的图象,只需将f(x)的图象( )个单位.
f′(x)的图象,只需将f(x)的图象( )个单位.
A.向右平移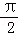 | B.向左平移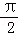 |
C.向右平移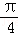 | D.向左平移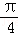 |
曲线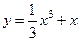 在点
在点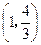 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )
A.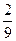 |
B.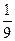 |
C.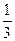 |
D.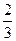 |
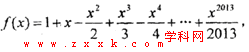 设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b
设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b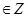 ) 内,,则x2+y2=b-a的面积的最小值为( )
) 内,,则x2+y2=b-a的面积的最小值为( )
 是
是 的导函数,
的导函数,