题目内容
已知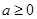 ,函数
,函数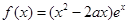 ,若
,若 在
在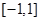 上是单调减函数,则
上是单调减函数,则 的取值范围是( )
的取值范围是( )
A.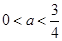 | B.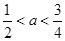 | C.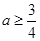 | D.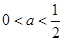 |
C
解析试题分析: ,由题意当
,由题意当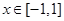 时,
时,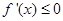 恒成立,即
恒成立,即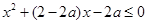 恒成立,即
恒成立,即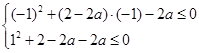 ,解得
,解得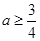 .选C.
.选C.
考点:函数的单调性,不等式恒成立问题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
设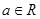 ,函数
,函数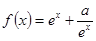 的导函数
的导函数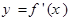 是奇函数,若曲线
是奇函数,若曲线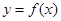 的一条切线的斜率为
的一条切线的斜率为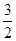 ,则切点的横坐标是( )
,则切点的横坐标是( )
A.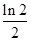 | B. | C.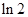 | D.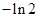 |
函数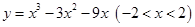 有( )
有( )
A.极大值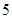 ,极小值 ,极小值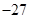 | B.极大值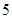 ,极小值 ,极小值 |
C.极大值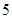 ,无极小值 ,无极小值 | D.极小值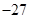 ,无极大值 ,无极大值 |
 是定义在
是定义在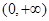 上的非负可导函数,且满足
上的非负可导函数,且满足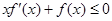 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( )
A.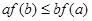 | B.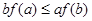 | C.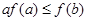 | D.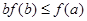 |
设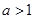 ,若曲线
,若曲线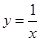 与直线
与直线 ,
,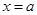 ,
,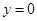 所围成封闭图形的面积为2,则
所围成封闭图形的面积为2,则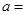 ( )
( )
| A.2 | B.e | C.2e | D.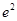 |
已知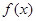 为
为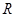 上的可导函数,且
上的可导函数,且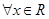 ,均有
,均有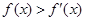 ,则以下判断正确的是
,则以下判断正确的是
A.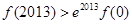 | B.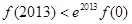 |
C.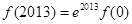 | D.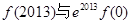 大小无法确定 大小无法确定 |
已知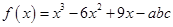 ,
,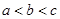 ,且
,且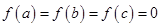 .现给出如下结论:
.现给出如下结论:
①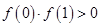 ;②
;②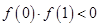 ;③
;③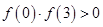 ;④
;④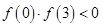 .
.
其中正确结论的序号是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
函数y=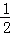 x2﹣lnx的单调递减区间为( )
x2﹣lnx的单调递减区间为( )
| A.(﹣1,1] | B.(0,1] |
| C.[1,+∞) | D.(0,+∞) |
下列求导数运算正确的是( )
A.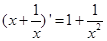 |
B.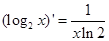 |
C.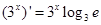 |
D.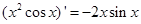 |