题目内容
已知f(x)=x2+ax+b,g(x)=x2+cx+d,又f(2x+1)=4g(x),且f′(x)=g′(x),f(5)=30,则g(4)= ( )
A.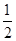 |
B.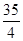 |
C.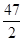 |
D.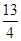 |
C
解析

练习册系列答案
相关题目
曲线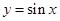 ,
,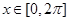 与坐标轴围成的面积( )
与坐标轴围成的面积( )
| A.4 | B.3 | C.2 | D.0 |
已知函数 的图象在点
的图象在点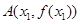 与点
与点 处的切线互相垂直,
处的切线互相垂直,
并交于点 ,则点
,则点 的坐标可能是( )
的坐标可能是( )
A. | B. | C. | D. |
设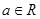 ,函数
,函数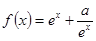 的导函数
的导函数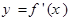 是奇函数,若曲线
是奇函数,若曲线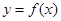 的一条切线的斜率为
的一条切线的斜率为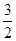 ,则切点的横坐标是( )
,则切点的横坐标是( )
A.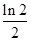 | B. | C.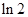 | D.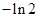 |
函数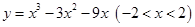 有( )
有( )
A.极大值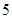 ,极小值 ,极小值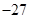 | B.极大值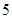 ,极小值 ,极小值 |
C.极大值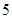 ,无极小值 ,无极小值 | D.极小值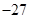 ,无极大值 ,无极大值 |
 是定义在
是定义在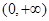 上的非负可导函数,且满足
上的非负可导函数,且满足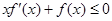 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( )
A.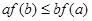 | B.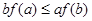 | C.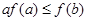 | D.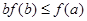 |
设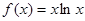 ,若
,若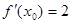 ,则
,则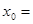 ( )
( )
A.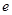 | B.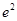 | C.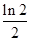 | D.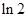 |
已知二次函数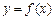 的图象如图所示,则它与
的图象如图所示,则它与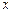 轴所围图形的面积为( )
轴所围图形的面积为( )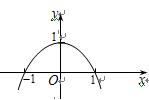
A.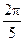 |
B.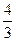 |
C.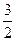 |
D.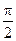 |
某公司规定:对于小于或等于150件的订购合同,每件售价为200元,对于多于150件的订购合同,每超过一件,则每件的售价比原来减少1元,则使公司的收益最大时应该订购的合同件数是( )
| A.150 |
| B.175 |
| C.200 |
| D.225 |