题目内容
 是
是 的导函数,
的导函数, 的图像如右图所示,则
的图像如右图所示,则 的图像只可能是( )
的图像只可能是( )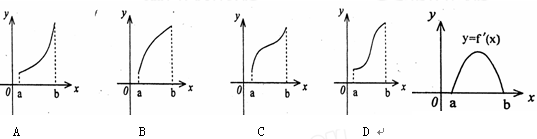
D
解析试题分析:根据导函数图像可知,导数值始终为大于等于零的数,说明原函数在 单调递增,并且导数值随着
单调递增,并且导数值随着 的增大,先变大,再变小,结合选项可知,A选项,导数值一直随
的增大,先变大,再变小,结合选项可知,A选项,导数值一直随 的增大而增大,不符合要求;B选项却是一直随
的增大而增大,不符合要求;B选项却是一直随 的增大而减小,不符合要求;而C选项,导数值先随
的增大而减小,不符合要求;而C选项,导数值先随 的增大而减小,后随
的增大而减小,后随 的增大而增大,不符合要求;而D选项,导数值随着
的增大而增大,不符合要求;而D选项,导数值随着 的增大,先变大,再变小,符合要求,故选D.
的增大,先变大,再变小,符合要求,故选D.
考点:1.导数的几何意义;2.函数的单调性与导数.

练习册系列答案
相关题目
已知函数 的图象在点
的图象在点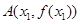 与点
与点 处的切线互相垂直,
处的切线互相垂直,
并交于点 ,则点
,则点 的坐标可能是( )
的坐标可能是( )
A. | B. | C. | D. |
 是定义在
是定义在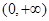 上的非负可导函数,且满足
上的非负可导函数,且满足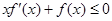 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( )
A.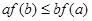 | B.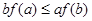 | C.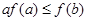 | D.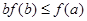 |
函数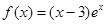 的单调递增区间是( )
的单调递增区间是( )
A.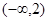 | B.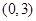 | C.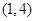 | D.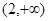 |
已知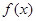 为
为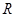 上的可导函数,且
上的可导函数,且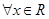 ,均有
,均有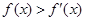 ,则以下判断正确的是
,则以下判断正确的是
A.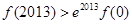 | B.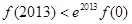 |
C.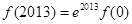 | D.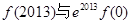 大小无法确定 大小无法确定 |
过点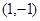 且与曲线
且与曲线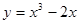 相切的直线方程为( )
相切的直线方程为( )
A.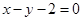 或 或 | B.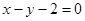 |
C.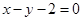 或 或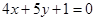 | D.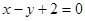 |
设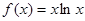 ,若
,若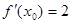 ,则
,则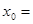 ( )
( )
A.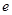 | B.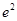 | C.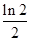 | D.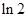 |
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)> 0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
过抛物线y=x2上的点M(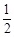 ,
, )的切线的倾斜角是( )
)的切线的倾斜角是( )
| A.30° | B.45° | C.60° | D.90° |