题目内容
已知矩阵M＝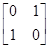
，N＝
，在平面直角坐标系中，设直线2x－y＋1＝0在矩阵MN对应的变换作用下得到的曲线F，求曲线F的方程．
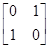，N＝，在平面直角坐标系中，设直线2x－y＋1＝0在矩阵MN对应的变换作用下得到的曲线F，求曲线F的方程．2x＋y＋1＝0
由题设得MN＝＝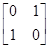
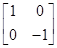.设(x，y)是直线2x－y＋1＝0上任意一点，
点(x，y)在矩阵MN对应的变换作用下变为(x′，y′)，
则有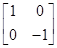
＝
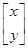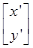，即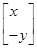
＝，
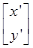所以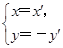
.
因为点(x，y)在直线2x－y＋1＝0上，从而2x′－(－y′)＋1＝0，即2x′＋y′＋1＝0.
所以曲线F的方程为2x＋y＋1＝0.
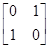
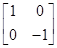＝.设(x，y)是直线2x－y＋1＝0上任意一点，点(x，y)在矩阵MN对应的变换作用下变为(x′，y′)，
则有
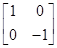
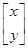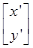＝，即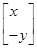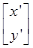＝，所以
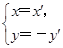.因为点(x，y)在直线2x－y＋1＝0上，从而2x′－(－y′)＋1＝0，即2x′＋y′＋1＝0.
所以曲线F的方程为2x＋y＋1＝0.
练习册系列答案
小学夺冠AB卷系列答案
相关题目
，则矩阵A的逆矩阵为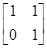 
；(2)M＝
.
+
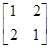=1在M-1的作用下的新曲线的方程.
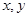，矩阵运算
都成立，则
.
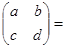之下的对应点的坐标为(－2，－4)，求m、k的值．